Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кумыкова С.К. 1 Халилова Л.А. 1

---

1 ФГБОУ ВПО «Кабардино-Балкарский государственный университет им. Х.М. Бербекова» Министерства образования и науки РФ

Для вырождающегося уравнения гиперболического типа изучена нелокальная краевая задача. Вопрос однозначной разрешимости задачи сведен к разрешимости интегральных уравнений Вольтерра второго рода при различных значениях параметров уравнения и операторов дробного интегро-дифференцирования.

Статья в формате PDF

2533 KB

краевая задача

оператор дробного интегро-дифференцирования

интегральное уравнение Вольтерра

1. Водахова В.А., Гучаева З.Х. Задача Дирихле для уравнения смешанного параболо–гиперболического типа с разрывными коэффициентами // Успехи современного естествознания. – 2013. – № 11. – С. 136–140.

2. Водахова В.А., Шамеева К.А. Задачи со смещением для системы уравнений первого порядка Лыкова // Известия Кабардино–Балкарского научного центра РАН. – 2013. – № 2 (52). – С. 3–7.

3. Лебедев Н.Н. Специальные функции и их приложения. – М.–Л.: Физматгиз, 1963. – 358 с.

4. Нахушев А.М. Задачи со смещением для уравнений в частных производных. – М.: Наука, 2006. – 287 с.

5. Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. – 688 с.

6. Смирнов М.М. Уравнения смешанного типа. – М.: Высшая школа. – 1985. – 304 с.

7. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для вырождающегося внутри области гиперболического уравнения // Вестник Самарского государственного университета. Естественнонаучная серия. – 2012. – №9 (100). – С.52–60.

8. Репин О.А., Кумыкова С.К. Нелокальная задача с дробными производными для уравнения смешанного типа // Известия высших учебных заведений. Математика. – 2014. – № 8. – С.79–85.

9. Репин О.А., Кумыкова С.К. Задача с обобщенными операторами дробного интегро–диференцирования произвольного порядка // Известия высших учебных заведений. Математика. – 2012. – №12. – С. 59–71.

10. Репин О.А., Кумыкова С.К. Внутреннекраевая задача с операторами Сайго для уравнения Геллерстедта // Дифференциальные уравнения. – 2013. – Т.49. – С.1340–1349.

Теория краевых задач для вырождающихся и смешанного типов уравнений в настоящее время является одним из важнейших разделов теории дифференциальных уравнений в частных производных и привлекает к себе внимание многих исследователей. За последние годы особенно интенсивно ведутся исследования задач со смещением и задач типа задачи Бицадзе – Самарского, что можно обосновать как внутренними потребностями обобщения классических задач для уравнений математической физики так и прикладным значением и связью с задачами газовой динамики, теории теплопроводности, теории упругости, теории плазмы, математической биологии и многими другими вопросами механики.

Для вырождающихся гиперболических и смешанного типов уравнений исследовались задачи, когда на характеристической части границы области задавалось нелокальное условие, поточечно связывающее значение решения или производная от него, вообще говоря, дробной определенного порядка, зависящего от порядка вырождения уравнения. Работ, посвященных исследованию случаев, когда в краевых условиях присутствуют дробные производные и интегралы произвольных порядков, не зависящих от порядка вырождения уравнения, сравнительно мало.

Цель исследования: Для вырождающегося гиперболического уравнения исследовать влияние порядков операторов дробного интегро-дифференцирования в краевом условии и коэффициента при младшей производной в уравнении на однозначную разрешимость задачи.

Постановка задачи. Рассмотрим уравнение

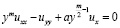, (1)

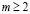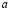
где , 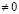– вещественная постоянная, в конечной области W, ограниченной характеристиками

,

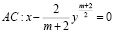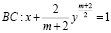
уравнения (1) и отрезком 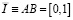прямой .

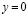Задача. Найти регулярное в области W решение 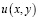уравнения (1) из класса 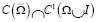, удовлетворяющее краевым условиям

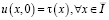(2)

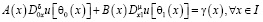, (3)

где 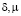– любые вещественные числа, 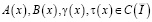, причем 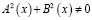, , 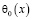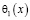– точки пересечения характеристик уравнения (1), выходящих из точки 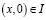с характеристиками AC, DC соответственно; 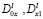– операторы дробного в смысле Римана-Лиувилля интегро-дифференцирования [5].

Задача (1) – (3) относится к классу краевых задач со смещением [4], исследованием которых для вырождающихся гиперболических и смешанного типов уравнений занимались многие авторы [1, 2, 4, 7–10].

Доказательство однозначной разрешимости задачи

При 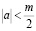решение задачи Коши для уравнения (1) имеет вид [6]

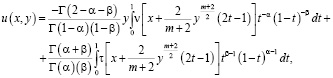(4)

а при

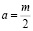
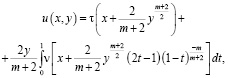(5)

где 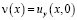; ; 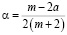; 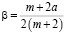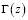– гамма функция Эйлера [3].

Удовлетворяя (4) краевому условию (3), получим интегральное уравнение относительно:

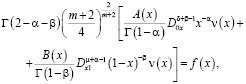(6)

где

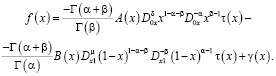
Теорема 1. Пусть 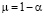, , 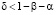, 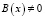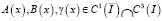. Тогда решение задачи (1) – (3) существует и единственно.

Действительно, при выполнении условий теоремы 1, уравнение (6) примет вид

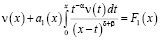, (7)

где

,

.

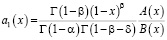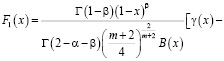
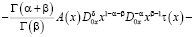
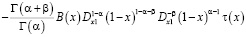Чтобы определить гладкость правой части уравнения (7) заметим, что [5]

,

,

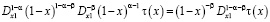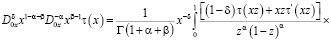
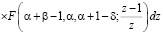где 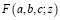– гипергеометрическая функция Гаусса [5].

Отсюда можно заключить, что

,

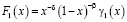где 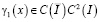– известная функция.

Пусть 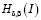класс функций 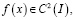могущих при 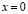обращаться в бесконечность порядка 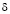, а при 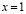в бесконечность порядка .

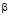Лемма. Пусть выполнены условия теоремы 1. Тогда уравнение (7) имеет единственное решение в классе функций .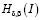

Доказательство леммы проведено применением к уравнению (7) метода последовательных приближений [9].

По найденному 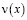и известному 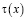решение задачи (1) – (3) определяется по формуле (4).

В случае 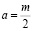, удовлетворяя (5) условию (3), вопрос существования решения задачи (1) – (3) эквивалентно редуцируется к разрешимости интегрального уравнения

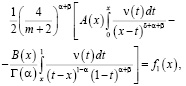(8)

где

.

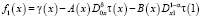Пусть 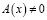. Подействовав на обе части (8) оператором 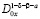, получим

,

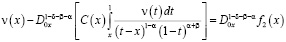где обозначено

, .

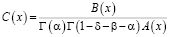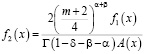Последнее уравнение в результате ряда преобразований сводится к уравнению Фредгольма второго рода относительно 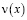со слабой особенностью в ядре

,

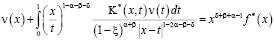где 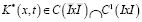, 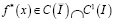– известные функции.

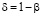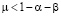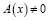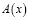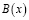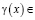
Теорема 2. Пусть , , , , , , 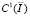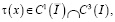тогда решение задачи (1) – (3) существует и единственно.

Доказательство, как и в случае теоремы 1, проводится путем редукции вопроса существования решения задачи (1)–(3) к разрешимости уравнения Вольтерра второго рода относительно 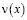со слабой особенностью в ядре и непрерывной правой частью.

Библиографическая ссылка