Разнообразные рейтинги широко используют для оценивания как общего места университетов в мировой и региональных системах высшего образования, так и их позиций по отдельным направлениям деятельности. Рейтинги университетов России, Украины и других постсоветских государств начали рассчитывать относительно недавно. Поэтому методики их составления вызывают много вопросов. Их разработчики ссылаются на использование мирового опыта с учетом местной специфики. Однако качество рейтингов должно подтверждаться не только воспроизводством методик, но и качественным подобием результатов. В частности, подобием их статистических характеристик.
Поэтому целью нашей работы было определение отдельных статистических свойств ведущих рейтингов университетов мира. При этом имелось в виду, что полученные результаты могут быть использованы в качестве некоторых эталонных требований, которым должны соответствовать вновь разрабатываемые рейтинги. С другой стороны, предполагалась необходимость проверки того, насколько сами «эталоны» соответствуют априорным требованиям к подобным показателям.
Для анализа мы использовали рейтинги, предполагающие получение числовых оценок как частных, так и итоговых показателей, т.е., главным образом рейтинги первой группы. В качестве основных анализируемых характеристик брали эмпирические функции распределения.
Распределение показателей рейтингов можно охарактеризовать такими свойствами: характер распределения (однородное или неоднородное); симметрия распределения (симметричное или асимметричное); ширина распределения (стандартное отклонение).
По нашему мнению, существуют некоторые априорные требования, которым должно удовлетворять распределение показателей качественного рейтинга. В первую очередь, это удовлетворительная «разрешающая способность», т.е. способность отличать друг от друга университеты, занимающие любые позиции в рейтинге. Отсюда следует, что коэффициент асимметрии распределения должен быть близок к нулю, среднее арифметическое близко к середине интервала оценок, а стандартное отклонение должно быть в пределах 0,18-0,25 от разницы между максимальным и минимальным значениями показателя для рейтингов, которые учитывают около 100 вузов; 0,15-0,20 - в случае 200 вузов и 0,13-0,19 для 500 вузов. Последние требования можно получить из свойств нормального распределения. В случае, если рейтинговые баллы подчиняются другому закону распределения они должны быть скорректированы.
Полученные нами результаты показывают, что даже для ведущих рейтингов эти требования не выполняются или выполняются не в полной мере. На рис. 1 показаны функции распределения показателей трех рейтингов - ARWU-2004, Times-2007 та ТОП200 университетов Украины - 2008. В таблице 1 приведены характеристики соответствующих распределений. Исходные данные взяты из источников [1-3].
Таблица 1
Характеристики распределения показателей рейтинга
|
Среднее арифметическое |
Коэффициент асимметрии |
Нормированное |
|
|
ARWU (2004-2009) |
36-38 |
1,78-1,95 |
0,17-0,19 |
|
Times (2007-2011) |
49-52 |
0,33-0,57 |
0,21-0,22 |
|
ТОП200 (2007-2009) |
8-18 |
2,7-4,2 |
0,12-0,14 |
Для представленных на рис. 1 рейтингов ARWU и Times распределение показателей является неоднородным и может быть представлено в виде суммы двух нормально распределенных компонент:
F(R) = 0,59N (29,3;3,5) + 0,49N (47,8;12,9)
F(R) = 0,601N (404;90) + 0,399N (678;78)
где N(a,b) - функция нормального распределения с математическим ожиданием a и стандартным отклонением b.
Распределение показателей рейтинга ТОП-200 университетов Украины описывается однородным логнормальным законом:
F(R) = L (2,11;0,582).
Приведенные данные свидетельствуют о том, что рейтинг Times удовлетворительно соответствует всем названным априорным требованиям. Рейтинг ARWU соответствует им по ширине распределения и не соответствует по его центру и коэффициенту асимметрии. Рейтинг ТОП200 университетов Украины не соответствует ни одному критерию и существенно отличается от остальных по виду распределения.
Другим важным результатом является то, что распределение показателей ведущих рейтингов является неоднородным. Основную причину этой неоднородности можно увидеть из рис. 2, где показаны функции распределения для отдельных составляющих рейтинга Times-2007.
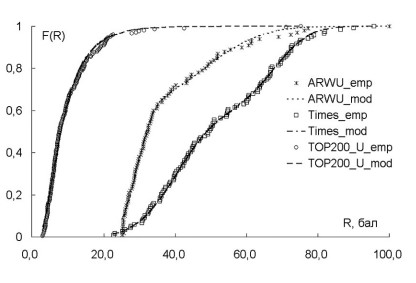
Рис. 1. Функции распределения рейтингов (для ARWU взяты первые 100 университетов; для Times приведено значение R/10)
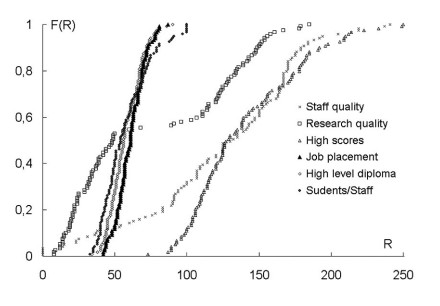
Рис. 2. Функции распределения для отдельных составляющих рейтинга Times-2007
Видно, что основной причиной является расслоение вузов по качеству научных исследований.
Таким образом, полученные результаты показывают, что рейтинг Sunday Times в наибольшей степени соответствует сформулированным априорным критериям и может быть использован в качестве некоторого эталона с точки зрения статистических свойств его показателей.
Список литературы
- The Sunday Times University Guide // http://extras.timesonline.co.uk/stug/universityguide.php
- О. Леновицкая. «Топ 200 Украина» в 2009 году // http://www.zn.ua/3000/3300/69717
- Academic Ranking of World Universities - 2010 // http://www.arwu.org/ARWU2010.jsp
Библиографическая ссылка
Бахрушин В.Е. СТАТИСТИЧЕСКИЙ АНАЛИЗ УНИВЕРСИТЕТСКИХ РЕЙТИНГОВ // Успехи современного естествознания. – 2010. – № 12. – С. 118-119;URL: https://natural-sciences.ru/ru/article/view?id=15473 (дата обращения: 26.04.2024).



