Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Многокомпонентные растворы электролитов являются наиболее распространенными объектами химической технологии. Однако оптимальный подбор компонентов для получения электролитных систем с требуемыми физико-химическими и электрохимическими параметрами является сложной задачей. Так, при исследовании электропроводности смесей электролитов необходимо учитывать, что даже в отсутствие химического взаимодействия между ионами закон независимого движения Кольрауша строго выполняется только при бесконечном разбавлении. Согласно теории Онзагера и Фуосса [6], в растворах смесей электролитов, если сравнивать их с индивидуальными растворами, меняются силы релаксационного торможения. Межионные же взаимодействия в смеси электролитов уменьшают различие в подвижностях одноименнозаряженных ионов, а увеличение концентрации смеси приводит к росту ассоциаций ионов, что приводит к увеличению отклонений от аддитивности и все закономерности еще более усложняются [1, 8]. Таким образом, можно сделать вывод, что, несмотря на определенные успехи в развитии теоретических представлений, современная теория растворов смесей электролитов разработана недостаточно, а используемые теоретические модели для решения данной задачи относительно точны в области малых концентраций и имеют значительные расхождения в области высоких концентраций [5, 7, 9].

В работах [2, 3] показана возможность применения плазменной модели состояния вещества к совокупности ионов в растворах слабых и сильных электролитов, поскольку растворы электролитов по основным параметрам газовой и твердотельной плазмы занимают промежуточное положение по пространственно-временным масштабам разделения зарядов, плазменному параметру и условию квазинейтральности. Полученные результаты позволили рассчитывать теоретически, без привлечения произвольных подгоночных параметров все диссипативные свойства растворов электролитов (электропроводность, диффузия, вязкость, теплопроводность) в широком диапазоне изменения концентраций в удовлетворительном соответствии с экспериментально определенными литературными данными с точностью от 1 до 2 %. Авторами было получено уравнение для расчета электропроводности в приближении плазмоподобного состояния ионов в растворах электролитов в виде

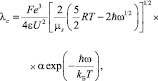(1)

где концентрация электролита включена в значение потенциальной энергии взаимодействия частиц, определяемой выражением

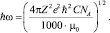
Таким образом, уравнение для расчета электропроводности индивидуальных растворов электролитов имеет вид

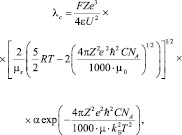(2)

где F – постоянная Фарадея; Z – эффективный заряд; e – элементарный заряд; e – диэлектрическая постоянная среды; R – универсальная газовая постоянная; T – температура в К; h – постоянная Планка; С – концентрация электролита в моль/л; NA – постоянная Авогадро; kБ – постоянная Больцмана; U – энергия водородной связи; µ0 – приведеннная масса несольватированных ионов; µs – приведенная масса сольватированных ионов; a – степень диссоциации, для сильных электролитов степень a = 1, а для слабых электролитов возможно определение a из закона разбавления Оствальда по известным значениям Kд:

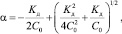
где С0 – исходная концентрация в моль/л.

Предлагаемое уравнение (2) для индивидуальных растворов электролитов в водных и неводных средах объясняет λ практически во всем диапазоне концентрации.

В настоящей работе для решения проблемы теоретических оценок электропроводности смесей электролитов с различными эквивалентными концентрациями С1, С2, ..., Сn предлагается ввести мольные доли ионов для смесей электролитов в состав приведенных масс сольватированных и несольватированных ионов, поскольку движения различных ионов в смеси электролитов являются сопряженными и коррелированными [4]:

С = С1 + С2 +...+ Сn;

1/µ0 = N1/m1 + N2/m2 +.. + Nn/mn; (3)

1/µs = N1/ms1 + N2/ms2 +...+ Nn/msn, (4)

где N1, N2, ..., Nn – мольные доли ионов:

N1 = C1/C; N2 = C2/C; ...; Nn = Cn/C,

m1, m2, ..., mn – массы несольватированных ионов в смеси; ms1, ms2, ..., msn – массы сольватированных ионов в смеси, рассчитанные по уравнению

ms = Мns + m,

где М – молярная масса растворителя; m – масса несольватированного иона; ns – cольватное число. Определение сольватных чисел отдельных ионов возможно на основе следующих рассуждений.

Ион с зарядом Zie взаимодействует с ns молекулами растворителя, имеющими дипольный момент р и дипольное расстояние R0. Такое взаимодействие является ион-дипольным. Потенциалы иона и диполя при этом равны соответственно

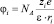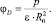и (5а)

Их потенциальные энергии имеют следующий вид:

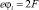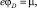и (5б)

где m – химический потенциал молекулы растворителя; F – изохорно-изотермический потенциал или свободная энергия.

Для ион-дипольного взаимодействия можно записать первое начало термодинамики в виде

TdS + µdN = dU + A,

где А = pdE – есть работа, совершаемая ионом по ориентации ns молекул растворителя в сольватный комплекс под действием поля иона Ев. Тогда имеет место следующее выражение:

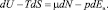(6)

Значение этой работы pdE можно установить из выражения термодинамики диэлектриков во внешнем поле Ев в виде

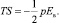(7)

Тогда

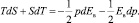
При p и s = const имеет место

(8)

Подставляя это значение pdE в уравнение (6), получим

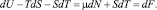(9)

Значение SdT можно установить из определения:

dU = dF + SdT.

Выразив из этого выражения SdT и подставив в уравнение (9), получим

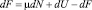
или, иначе,

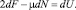(10)

Здесь изменение внутренней энергии есть

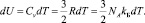
Интегрирование уравнения (10) приводит к виду

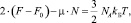
где 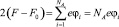и 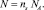Тогда с учетом выражений (5) получим следующее уравнение:

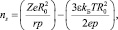(11)

где Z – заряд иона; R0 – радиус молекулы растворителя; r – радиус иона; р – дипольный момент; е – заряд электрона; e – диэлектрическая постоянная среды; Т – температура; kБ – постоянная Больцмана.

Результаты рассчитанных величин сольватных чисел ионов и их сопоставление с литературными данными приведены в табл. 1.

Таблица 1

Данные теоретических оценок сольватных чисел ионов в воде при Т = 298 К

Полученные величины сольватных чисел далее используем при расчете электропроводностей электролитных систем.

В связи с тем, что в справочной литературе отсутствуют достоверные значения электропроводностей смесей электролитов, получены их экспериментальные значения и сравнены с соответствующими данными теоретических расчетов.

Таблица 2

Эквивалентная электропроводность λ (Ом-1·см2·моль-1) смеси водных растворов

Для измерения удельной электрической проводимости растворов электролитов использовалась термостатируемая кондуктометрическая ячейка, подключенная к кислородомеру «Анион-410» фирмы ИНФРА-СПАК-АНАЛИТ (Россия), где в основе измерения удельной электрической проводимости раствора положен принцип измерения проводимости раствора в ячейке Кольрауша. Для обеспечения достоверности и точности измерений использовался комбинированный выносной датчик ДКВ-1, являющийся кондуктометрическим первичным преобразователем, представляющий собой четырехэлектродную ячейку погружного типа со стальным электродом марки 12Х18Н9Т.

В задачу экспериментальной части работы входило измерение электропроводности смесей растворов электролитов при 9 различных концентрациях для 171 смеси двойных систем 19 различных составов.

В табл. 2 представлены некоторые результаты экспериментально полученных и теоретически оцененных по уравнению (2) электрических проводимостей смесей растворов электролитов с учетом мольных долей каждого компонента.

Сопоставление рассчитанных величин электропроводностей с экспериментальными данными для тройных водных систем, в которых два электролита имеют общий ион, показывает лучшее соответствие. В случае двух электролитов, не имеющих общего иона, наблюдается различие рассчитанных и экспериментальных значений электропроводности. Это явление объясняется, по-видимому, тем, что в таких растворах кроме исходных электролитов образуются и перекрестные соединения.

Таким образом, теоретически оцененные величины электропроводностей смесей растворов электролитов в соответствии с уравнением (2) и учетом мольных долей ионов, хорошо согласуются с экспериментальными данными.