Совокупность экспериментальных данных указывает на то, что белковые молекулы должны быть организованы определенным образом, позволяющим проявлять им весьма специфические структурные и функциональные свойства. Более полувека назад Анфинсен предположил, что структурные и функциональные свойства белков определяются их аминокислотной последовательностью: «информация... о нативных вторичных и третичных структурах белков, содержится в их аминокислотной последовательности» [1]. В соответствии с этим утверждением аминокислотная последовательность должна полностью определять пространственную организацию белка.
Однако в настоящее время методы анализа белковых последовательностей позволяют выявлять только трансмембранные участки, кластеры гидрофобных остатков (предположительно – те, которые участвуют в формировании гидрофобных ядер белковых глобул), а также более или менее надежно идентифицировать элементы вторичной структуры белков. Целый ряд других особенностей организации трехмерной структуры белков при анализе их первичных структур выявить не удается. В ряде работ предпринимались попытки оценить степень упорядоченности аминокислотных остатков в первичных структурах белков, которые привели к очень низким ее значениям [8, 9]. Более того, авторы работы [5] пришли к выводу, что «аминокислотные последовательности белков представляют собой слабо отредактированные случайные гетерополимеры». Эти результаты противоречат наблюдаемым свойствам белков, таким как способность к самоорганизации, селективное связывание с регуляторами и субстратами (в случае ферментов), высокая эффективность каталитических реакций и т.д. Задача требует своего решения. Очевидно, что большинство характерных свойств белков связаны с физико-химическими свойствами аминокислотных остатков, и, следовательно, необходимо найти такую статистическую модель, которая могла бы позволить описать физические и химические свойства аминокислотных остатков с помощью их статистических параметров, которые можно получить из полипептидных цепей. В работе [6] было показано, что физико-химические свойства аминокислотных остатков можно адекватно описывать, если рассматривать не только отдельные аминокислотные остатки, но и их непосредственное окружение в первичной структуре. Для того чтобы определить размер окрестности, которую необходимо учитывать, была исследована позиционная информационная энтропия в наборах негомологичных белковых последовательностей.
Базы данных
В качестве объектов исследований использовались последовательности из баз данных NRDB [3] трех различных релизов: NRDB 30, NRDB 60 и NRDB 90.
- Исходная база данных NRDB 30 содержит 192,518 белковых последовательностей.
- Исходная база данных NRDB 60 содержит 252,926 белковых последовательностей.
- Исходная база данных NRDB 90 содержит 534,936 белковых последовательностей.
Теоретическое обоснование метода
Чтобы получить искомую оценку области, адекватную особенностям природных полипептидных цепей (размер «информационной единицы») для аминокислотных последовательностей из различных релизов базы данных NRDB, были рассчитаны вероятности (Pk) появления различных пар аминокислотных остатков с фиксированным числом позиций (k) между ними (рис. 1). В каждой такой паре остатков один остаток (в положении n) будем называть «корневым», а второй остаток в паре (в положении n + k) – «переменным». В процессе расчета «корневой» остаток последовательно смещается от позиции 1 в аминокислотной последовательности белка до остатка номер L-k, где L представляет собой общее количество остатков в белке.
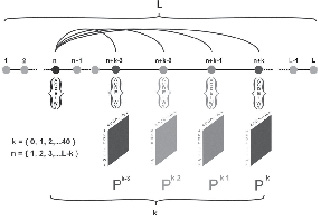
Рис. 1. Схема анализа базы данных, описывающей белковые последовательности, выполненного для получения матриц частот встречаемости пар аминокислотных остатков. Положение «корневого» остатка в паре изменяется от 1 до L-k (где L представляет собой общее количество остатков в белке. «Переменный» остаток рассматривается в позициях от n + 1 до n + k при положении «корневого» остатка в позиции n последовательности белка
«Переменный» остаток рассматривается в позициях от n + 1 до n + k при положении «корневого» остатка в позиции n последовательности белка. При расчете вероятностных матриц Pk были использованы все аминокислотные последовательности белков, входящие в рассматриваемый релиз базы NRDB. В результате были сформированы 50 матриц размером 20х20 (k = 1 ... 50). Размер матриц определяется числом канонических аминокислотных остатков, встречающихся в белковых последовательностях. Полученные матрицы Pk характеризуют только расстояние между аминокислотными остатками в паре и не зависят от каких-либо других параметров исследуемых белковых последовательностей.
Для того, чтобы охарактеризовать расстояние k между остатками в паре, была рассчитана информационная энтропия Шеннона Sk для матриц Pk по формуле [7]
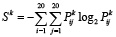. (1)
В результате были получены 50 значений информационной энтропии, по одному значению для каждой матрицы. Матрицы Pk и значения информационной энтропии Sk были получены для всех трех рассмотренных релизов базы данных NRDB. Исходя из предположения, что аминокислотные остатки, находящиеся в соседних положениях (k = 1), наиболее скоррелированы между собой в паре по типу, и, следовательно, матрица P1 имеет минимальное значение энтропии S1, все остальные значения Sk были пронормированы на эту величину. График нормированных значений информационной энтропии Sk/S1 для различных релизов NRDB приведен на рис. 2. Видно, что полученные кривые имеют S-образную форму и сходны для различных релизов NRDB. Для трех представленных зависимостей наблюдается почти полное совпадение локальных максимумов и минимумов. Это позволяет предположить, что полученные данные представляют собой специфические характеристики природных полипептидных цепей как класса молекул и не зависят от размера и состава анализируемых наборов данных.
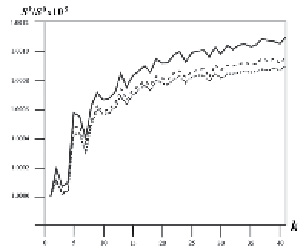
Рис. 2. Зависимость нормированной информационной энтропии Sk/S1 от расстояния между аминокислотными остатками (k) в паре. Точечная линия обозначает зависимость, полученную для NRDB релиза 90, штриховая – для релиза 60 и сплошная – для релиза 30
Очевидно, что при росте k величина Sk/S1 увеличивается и наблюдается падение амплитуды колебаний. При k > 30 функция Sk/S1 почти достигает плато.
Наиболее интересной особенностью полученной зависимости является то, что на расстоянии между аминокислотными остатками k = 5 начинается устойчивый рост значений нормированной информационной энтропии Sk/S1. Минимальные значения информационной энтропии наблюдаются при значениях k от 1 до 4. Основываясь на этих данных, мы предположили, что пентапептидные фрагменты (k = 4) можно рассматриваеть как единицы структурной огранизации белка. Далее такие структурные единицы белков мы будем называть «информационными единицами» («information units», IU).
Метод анализа информации о структуре белка
Основываясь на предложенном приближении, белковую последовательность можно рассматривать не как последовательность аминокислотных остатков, а как систему последовательно расположенных и перекрывающихся (со сдвигом на одну позицию) информационных единиц. Для использования предложенного приближения при анализе белковых последовательностях был разработан специальный алгоритм.
Пусть первичная структура белка есть последовательность аминокислот Ai,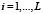 
, где аминокислоты могут быть 20 типов.
В соответствии с предложенной парадигмой структурной организацией белков, каждой последовательности аминокислот, имеющей длину M = 5, сопоставим величину, определенную следующим образом. Возьмем базу данных NRDB, состоящую из первичных структур белков. Последовательности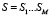 
из M аминокислот сопоставим частоту f(S) встречаемости в качестве всевозможных подпоследовательностей стоящих рядом аминокислот во всех белках из рассмотренной базы данных.
Выберем теперь набор последовательностей S' длины M, отличающихся от S заменой одной аминокислоты (таких последовательностей существует 20M штук). Последовательности S' сопоставим соответствующую частоту f(S'). Проведем суммирование по всем возможным последовательностям S', получаемым заменой одной аминокислоты и отвечающим S. В результате получим функцию
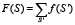. (2)
Теперь для данного рассматриваемого белка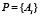 
длины L мы будем рассматривать всевозможные подпоследовательности 
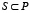длины M стоящих рядом аминокислот, таких подпоследовательностей в белке длины L будет 
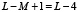штук. Введем нумерацию этих последовательностей 
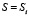длины 5 по их центрам i, таким образом, 
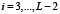, и рассмотрим функцию
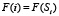, (3)
то есть суммарную частоту встречаемости в базе данных NRDB всевозможных подпоследовательностей S’ длины 5, отвечающих подпоследовательности S с центром в аминокислоте с номером i в данном белке.
Ранее для белка из L аминокислот была построена функция F(i),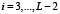 
частоты встречаемости в базе данных подпоследовательности длины 5. Сопоставим этой функции гистограмму, то есть функцию F(x) на отрезке 
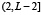, принимающую для 
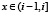значение 
.
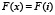Построим теперь по гистограмме F(x) функцию нелинейного сглаживания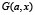 
по следующему правилу.
Рассмотрим сглаживающую функцию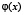 
– непрерывную функцию с носителем на отрезке 
, 
, 
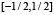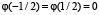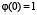, принимает положительные значения в интервале 
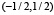, монотонно растёт на 
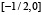, монотонно убывает на 
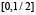, график функции симметричен относительно отображения относительно прямой x = 0. Мы также считаем, что функция гладкая, причём производная не обращается в нуль на отрезках 
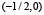и 
.
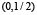В качестве сглаживающей функции можно выбрать соответствующим образом сдвинутую и перерастянутую гауссовскую функцию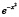 
, график которой обрезан на половине высоты.
Будем также рассматривать сдвиги и растяжения сглаживающей функции
, (4)
где a ≥ 1. Функция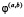 
имеет носитель в отрезке 
.
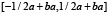Определим теперь функцию нелинейного сглаживания G(x, a) для функции F по следующей формуле
, 
, 
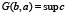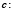
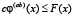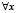. (5)
Таким образом, G(b, a) есть максимальная высота supc сглаживающей функции шириной a с центром носителя в точке b, которую можно вписать в гистограмму F. Параметр a назовём масштабом сглаживания.
Носитель функции G(x, a) имеет следующий вид. Функция G(x, a) может быть отлична от нуля при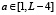 
, 
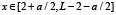. Таким образом, функция нелинейного сглаживания имеет носитель, являющийся подмножеством треугольника на плоскости с координатами (x, a) с вершинами 
, 
, 
.
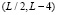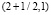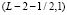Совокупность полученных значений сглаживающей функции G(x, a) назовем информационной структурой исследуемого белка.
Точность результатов, полученных методом АНИС
Мы использовали метод «бутстреп» [2, 10], чтобы создать 100 тестовых наборов белковых последовательностей на основе ранее описанной базы данных NRDB релиз 90.
Эти тестовые наборы были использованы для проверки устойчивости результатов, получаемых АНИС методом [4]. На основе этих тестовых наборов была получена статистика встречаемости для IU. Эта статистика была использована для расчета информационных структур 100 случайно выбранных белковых последовательностей длиной более 300 аминокислотных остатков. На рис. 5 представлен график среднего отклонения в положениях локальных максимумов и локальных минимумов сглаживающей функции G(x, a) при различных значениях масштаба сглаживания a.
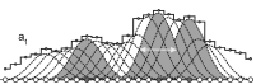
а)
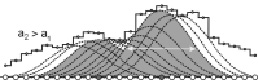
б)
Рис. 3. Нелинейное сглаживание «популяции» функции эквивалентных: IU. а) с масштабом сглаживания a1; б) с масштабом сглаживания a2 > a1. Масштабы сглаживания a1 и a2 показаны горизонтальными стрелками. Пунктирные и сплошные линии показывают все возможные функции сглаживания для рассматриваемого фрагмента белковой последовательности. Локальные максимумы сглаживающих функций G(i, a) выделены серым фоном, а заполненные кружки показывают центральные аминокислотные остатки для таких сглаживающих функций
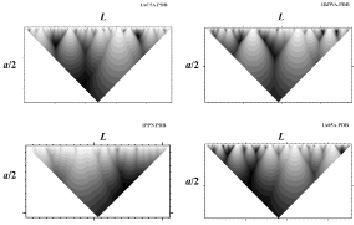
Рис. 4. Примеры расчетов информационных структур для различных белков. 1AC5A.PDB – KEX1(DELTA)P (цепь А) из Saccharomyces Cerevisiae, 1BJWA – аспартатаминотрансфераза (цепь А) из Thermus Thermophilus, 1PPN – моноклинный папаин из Carica Papaya, 1A05A – 3-изопропилмалат дегидрогеназа (цепь А) из Thiobacillus Ferrooxidans, a – масштаб сглаживания, L – число остатков в белковой последовательности
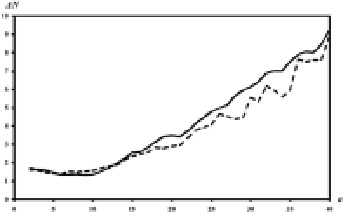
Рис. 5. График соотношения между ΔN и a. ΔN – среднее отклонение сглаживающей функции G(i, a), выраженное в количестве позиций, для локальных максимумов (сплошная линия) и локальных минимумов (пунктирная линия), a – масштаб сглаживания, полученный для 100 случайно выбранных белковых последовательностей
На рис. 5 показано, что для масштаба сглаживания a, находящегося в интервале значений от 2 до 12, среднее отклонение в позициях локальных максимумов и минимумов – примерно ± 2 позиции, и среднее отклонение растет по мере увеличения масштаба сглаживания. Максимальное среднее отклонение при a = 40 для обоих максимумов и минимумов – почти ± 9. Ошибка идентификации элементов информационной структуры изменяется от 1 до 3 позиций для значений масштаба сглаживания от 2 до 22, т.е. для фрагментов белковой последовательности длиной от 5 до 45 аминокислотных остатков.
Выводы
Анализ данных позиционной информационной энтропии позволил обосновать новую парадигму структурной организации белков, в которой элементарной структурной единицей является группа из пяти рядом стоящих аминокислотных остатков. Использование этой парадигмы позволило разработать новый метод анализа аминокислотных последовательностей белков, позволяющий выявлять иерархическую организацию в их первичной структуре.
Авторы благодарят коллектив Лаборатории химии протеолитических ферментов ИБХ РАН за полезное обсуждение работы и помощь в организации рабочего процесса.
Эта работа была поддержана Российской Академией Наук [грант по программе фундаментальных исследований в стратегических направлениях развития науки Президиума РАН «Фундаментальные проблемы математического моделирования» (код программы: II.4П), проект «Математическая модель пространственной организации природных полипептидных цепей на основе информационного контента первичной структуры»].