Введение
Одним из основных разделов современной теории дифференциальных уравнений с частными производными является теория уравнений смешанного типа. В настоящее время эта теория интенсивно развивается, так как появилось достаточно много прикладных задач, математическое моделирование которых обусловило исследование различных типов уравнений в рассматриваемой области изменения независимых переменных. Понятие уравнений смешанного типа в настоящее время включает всевозможные комбинации двух и более классических типов уравнений. Особый интерес представляют краевые задачи для уравнений с частными производными смешанного типа, так как они мало исследованы и находят применение в важных вопросах механики, физики и техники. Нелокальные краевые задачи для вырождающихся гиперболических и смешанного типов уравнений исследовались в работах [2-4], [5-9] и [11-13]. Подробная библиография содержится в [2].
Цель исследования: доказать существование решения задачи со смещением для параболо-гиперболического уравнения.
Постановка задачи.
Рассмотрим уравнение
в конечной области Ω, ограниченной отрезками АА0, ВВ0, А0В0 прямых х = 0, х = 1, y = 1 соответственно и характеристиками уравнения (1)
Пусть
Задача. Найти функцию u(x,y) со следующими свойствами:
2. u(x,y) – решение уравнения (1) при y ≠ 0;
3. u(x,y) удовлетворяет условиям
причем
где J – интервал 0 < х < 1 прямой y = 0; θ0(x), θ1(x) – точки пересечения характеристик уравнения (1), выходящих из точки (x,0) с характеристиками AC,BC.
Доказательство существования решения задачи.
Решение задачи Коши для уравнения (1) в области Ω2 при |λ| < 1 имеет вид [1]
где
Вычислим 
где Dlax – здесь и далее, операторы дробного в смысле Римана – Лиувилля интегро – дифференцирования [10].
Переходя в уравнении (1) к пределу при y → +0, получим соотношение между τ(x) и ν(x), принесенное из Ω1 на J: 
Проинтегрировав последнее трижды с учетом условий (2), будем иметь
Подставив u[θ0(x)], u[θ1(x)] и τ(x) из (5) в (3), получим уравнение относительно ν(x)
где
Из условий гладкости на известные функции следует, что 
Уравнение (6) после преобразований примет вид
где
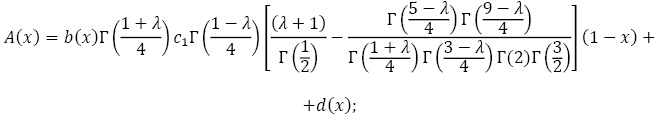
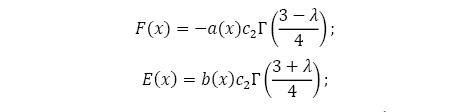
где F(a,b,c,z) – гипергеометрическая функция Гаусса [10].
Подействовав на обе части полученного уравнения оператором 
, окончательно получим уравнение Фредгольма второго рода
где
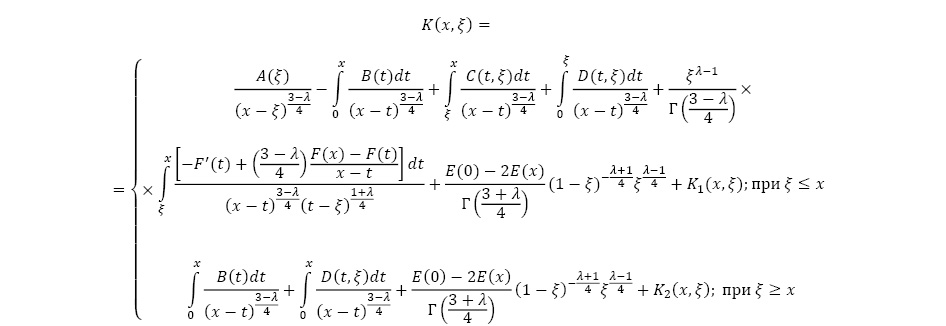
Таким образом, вопрос существования решения задачи (1) – (3) эквивалентен вопросу разрешимости интегрального уравнения Фредгольма второго рода (8) со слабой особенностью в ядре К(х,ξ). По найденному ν(х) можно определить τ(х) по формуле (5) и решение задачи (1) – (3) в области Ω2 по формуле (4), а в области Ω1 как решение задачи (1), (2), u(x,0) = τ(x) [2].