Множество технологических процессов связано с преобразованием тепловой энергии. Технологические процессы, выполняемые в нанотехнологиях, крайне чувствительны к выделению тепла, так как тепловые колебания отдельных атомов и структур атомов могут привести к нарушению работоспособности результата технологического процесса. Чтобы минимизировать влияние температуры на технологический процесс, нужно ввести в конструкции тех или иных нанотехнологических устройств тепловые трубки. Тепловые трубки позволяют отводить от рабочей зоны тепловые потоки высокой плотности (порядка нескольких киловатт на квадратный сантиметр) и – главное, с высокой скоростью, ограниченной лишь скоростью звука для газа внутри тепловой трубки.
Рассмотрим модификации устройств с помощью тепловых трубок на примерах устройств наноперемещения зонда.
Устройство наноперемещений зонда (рис. 1) содержит пьезопривод 1, выполненный из набора пьезоколец 2, между которыми расположены металлические кольца 3, тепловую трубку 4, закрепленную на свободном торце пьезопривода 1, зонд 5, установленный в тепловой трубке 4 и взаимодействующий с подложкой 6, тепловая трубка 4 связана с источником жидкого азота 7.
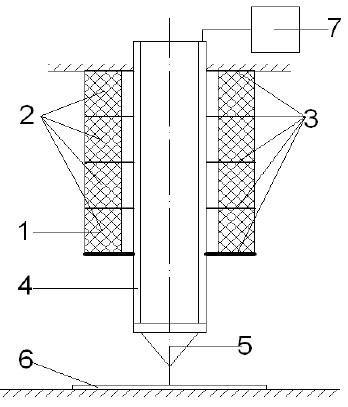
Рис. 1. Устройство наноперемещений зонда
Устройство наноперемещений зонда работает следующим образом.
При подаче напряжения на металлические кольца 3, происходит механическая деформация пьезопривода 1 из набора пьезоколец 2 вследствие обратного пьезоэффекта, при этом тепловая трубка 4, жестко связанная со свободным торцем пьезопривода 1, выполняет перемещение зонда 5 перпендикулярно подложке 6, в результате сил электрического взаимодействия зонда 5 и подложки 6 выполняется технологический процесс, при этом тепло из рабочей зоны зонда 5 тепловой трубки 4 к источнику жидкого азота 7.
Пьезопривод с тепловой трубой (рис. 2) содержит неподвижную направляющую 1, стол 2, на котором установлена подложка 3, пьезоэлектрический преобразователь 4, жестко связанный с неподвижной направляющей 1, зонд 5, жестко связанный с торцем тепловой трубки 6, которая в свою очередь жестко связана со свободным торцем пьезоэлектрического преобразователя 4, а так же связана с узлом подачи хладагента, дополнительно зонд 5 и подложка 3 связаны с усилителем сигналов 8 и блоком измерения 9.
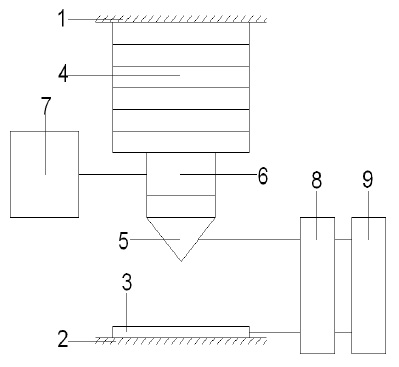
Рис. 2. Пьезопривод с тепловой трубой
Пьезопривод с тепловой трубой работает следующим образом.
При подаче напряжения на пьезоэлектрический преобразователь 4, зонд 5 перемещается перпендикулярно подложке 3 и выполняет технологический процесс. Вследствие действия эффекта Зеебека, в термопаре подложка-зонд начинает действовать ТЭДС, которую усиливает усилитель сигнала 8 и передает в блок измерения 9, который регистрирует температуру рабочей зоны. Отвод тепла от рабочей зоны и зонда 5 осуществляется посредством тепловой трубки 6, соединенной с узлом подачи хладагента 7.
Применение предложенных конструктивных усовершенствований позволяет эффективно отводить тепло из рабочей зоны, что в общем случае повышает точность выполнения технологических операций, а введение устройств контроля температуры рабочей зоны так же может позволить прекратить технологический процесс, чтобы избежать нарушений.
Для проектирования тепловых трубок и последующего их введения в нанотехнологические устройства, необходимо описать процессы, позволяющие достигать высокой эффективности теплоотвода.
Представим математически процесс переноса энергии и вещества в условиях ламинарного несжимаемого потока пара внутри цилиндрической тепловой трубы.
Запишем уравнения переноса пара:
![]()
![]()
![]()
здесь v – скорость переноса пара, ρп – плотность пара, Pп – давление пара, ηп – динамическая вязкость пара, Тп – температура пара, сп – теплоемкость пара, λ – теплопроводность пара, описание ![]() дано ниже.
дано ниже.
Уравнения переноса энергии в пористом фитиле, насыщенном конденсатом
![]()
![]()
здесь сж – теплоемкость жидкости, П – пористость фитиля, Vж – объем жидкости, ρж – плотность жидкости, Тж – температура жидкости, q – плотность теплового потока. Так же введен Λ – тензор теплопроводности капиллярно-пористого фитиля, насыщенного жидкостью, так как теплопроводность в осевом направлении фитиля отличается от его теплопроводности в радиальном направлении
![]()
Данная система из шести уравнений в общем случае описывает перенос тепловой энергии во внутреннем пространстве трубки, а именно в артерии и фитиле. Для полного описания переноса тепла необходимо дополнить данную систему уравнениями переноса тепла в оболочке трубы, а так же уравнениями фильрации жидкости в капиллярно-пористой среде фитиля.
Максимальное капиллярное давление, развиваемое в пористом фитиле, имеющем эффективный размер пор rэ
![]()
Перенос ламинарного потока жидкости в пористом фитиле в зависимости от вида фитиля определяется либо по закону Дарси (для жидкостей, подчиняющихся закону Навье-Стокса)
![]()
![]()
либо Пуазейля (одно из самых простых точных решений уравнений Навье-Стокса)
![]()
Кроме поля капиллярных сил на перенос жидкости оказывает влияние гравитационное поле, поэтому в выражение для определения ∆Рж необходимо ввести член ![]()
Кинетика фазового перехода жидкость-пар, т.е. скорость испарения и конденсации, может быть определена с помощью критерия Kn (число Кнудсена). Максимальный тепловой поток при испарении с плоской поверхности в вакуум
![]()
R0 – универсальна газовая постоянная, L – скрытая теплота парообразования. В ряде случаев перенос энергии и вещества в тепловых трубах может происходить при частичном осушении пористого фитиля.
В итоге расчет тепловой трубы основывается на уравнениях динамики потока жидкости и пара, описании кинетики фазовых переходов на поверхности раздела жидкость-пар, а так же уравнениях переноса энергии в артерии трубки, в каппилярно-пористой части (фитиле) и в самой оболочке трубы.
Поток жидкости в пористом теле фитиля должен быть более подробно, он может быть описан законом Дарси.
![]()
Проинтегрировав это уравнение, получаем перепад давления в двух точках фитиля. Проницаемость Kж зависит от пористости П фитиля и степени его насыщения жидкостью bж
![]()
При больших тепловых нагрузках насыщенность пористого фитиля жидкостью зависит от координаты. Пористый материал может быть охарактеризован следующими параметрами: размером пор d; линейным размером l пористого тела. В пределах этого размера берется осреднение по объему пористого тела.
Средняя объемная величина какой-то функции Ψ тензорного типа, характеризующей жидкость в пористом материале, определяется соотношением
![]()
при d<
Основное усредненное соотношение для характеристики жидкости в пористом теле имеет вид
поверхностный интеграл берется вдоль поверхности жидкости Si в зоне поверхности раздела жидкость – пар в объеме пористого фитиля; n1 - единичный вектор по нормали к поверхности элемента dS.
Это уравнение необходимо для вывода уравнения движения жидкости в пористом теле.
Третьей характеристикой пористого тела является дифференциальная кривая распределения поверхностной проницаемости f(K) (подобно кривой распределения пор по радиусу).
Для однородного материала такая кривая может быть представлена как дельта функция К или линейная комбинация этих функций.
![]() Ai удовлетворяет условию
Ai удовлетворяет условию
![]() N конечно.
N конечно.
Если f(K) не может быть представлена как конечное число функций, то материал неоднородный.
Если f(K) представлена одним членом – материал гомогенный.
Если материал описывается двумя или более функциями f(K) то он гетерогенный.
Если f(K) зависит от прямоугольных координат xi (i=1,2,3) и угловых координат Ψ, θ, то пористый материал является анизотропным. Если отсутствует зависимость от угловых координат – материал изотропный
![]()
В качестве теплоносителя в тепловых трубках можно применять множество жидкостей с низкой температурой испарения.
Из всего перечня наивысшая теплота испарения, как видно из таблицы 1, у самой распространенной жидкости - воды. Это наиболее эффективный теплоноситель работающий на испарение при реальных температурах в электронной аппаратуре [4].
Таблица 1
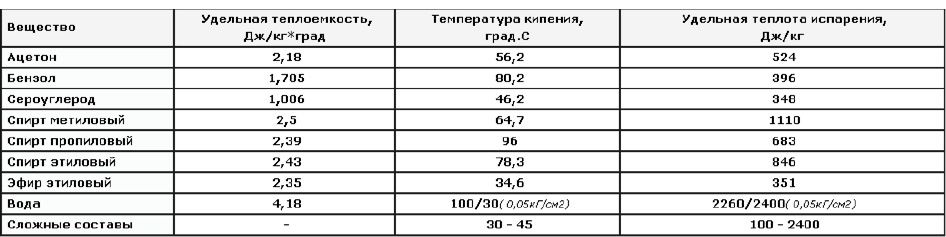
Следует отметить, что существуют современные компьютерные методы проектирования и анализа, которые могут быть применимы к задачам создания как отдельных тепловых трубок для нанотехнологических устройств, так и для проектирования этих устройств в целом.
Например, для расчета и описания течения ламинарного потока газа через артерию тепловой трубки может быть использован метод конечных объемов (МКО), развиваемый более 40 лет.
Для описания потока величины φ в объеме Ω, ограниченном поверхностью S с внешней нормалью ![]() , используется уравнение баланса [2].
, используется уравнение баланса [2].
В качестве φ можно в данном случае использовать внутреннюю энергию газа в артерии тепловой трубки. Существует несколько методов аппроксимации интегралов, но при использовании МКО сложно добиться точности численной схемы выше второго порядка.
Используя МКО возможно моделирование течения потока газа через артерию тепловой трубки, но остается открытым вопрос моделирования переноса энергии в пористом фитиле. Одним из новых методов моделирования динамических задач механики является метод подвижных клеточных автоматов (МПКА).
Для описания перемещения и поворота автоматов применяются уравнения механики Ньютона-Эйлера. В данном методе используются тензорные уравнения для описания поступательного, вращательного движений автоматов и их линейных деформаций [3].
Данный метод объединяет возможности методов молекулярной динамики и клеточных автоматов. Его ценность заключается в том, что с его помощью можно напрямую учитывать такие события в пористом фитиле как: перемешивание масс, эффект проникновения, фазовые превращения, капиллярное течение.
В заключении следует отметить, что существует фундаментальная теоретическая база для расчета тепловых трубок, а так же машинные приложения в виде метода конечных объемов и метода подвижных клеточных автоматов. Внедрение тепловых трубок в нанотехнологии позволит повысить точность и производительность выполнения технологических процессов.



