Введение
Современные компьютеры дали в руки исследователей эффективное средство для математического моделирования сложных задач науки и техники. Поэтому количественные методы исследования в настоящее время проникли практически во все сферы человеческой деятельности.
Реализация математических моделей на компьютере осуществляется с помощью методов вычислительной математики, которая непрерывно совершенствуется вместе с прогрессом в области информационно-коммуникационных технологии[1],[2]. Рассмотрим уравнение Лапласса
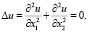 (1)
(1)
Будем искать его решение, непрерывное в прямоугольнике и
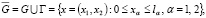
принимающее на границе Г заданные значения:
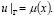 (2)
(2)
Задача, определяемая уравнением (1) и условием (2), называется задачей Дирихле (первой краевой задачей).
Постановка задачи.Для численного решения задачи (1), (2) введем в 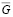 сетку
сетку
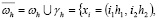
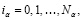
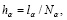
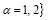
и обозначим через
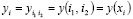
сеточную функцию, заданную на 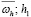 и
и 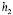 – шаги сетки по координатам
– шаги сетки по координатам 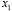 и
и 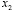 .
.
Чтобы написать разностную схему для (1), (2), аппроксимируем каждую из производных 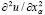 на трехточечном шаблоне, полагая
на трехточечном шаблоне, полагая
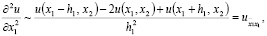
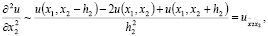
знак ~ означает аппроксимацию. Пользуясь этими выражениями, заменим (1) разностным уравнением
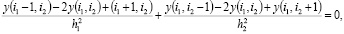 (3)
(3)
или, в сокращенной записи,
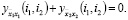
В безындексных обозначениях имеем
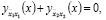
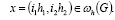 (4)
(4)
К этому уравнению надо присоединить краевые условия
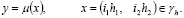 (5)
(5)
Граница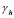 сетки состоит из всех узлов
сетки состоит из всех узлов 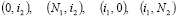 , кроме вершин прямоугольника (0, 0)
, кроме вершин прямоугольника (0, 0) 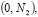
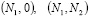 , которые не используются. Разностное уравнение (3) записано на пятиточечном шаблоне
, которые не используются. Разностное уравнение (3) записано на пятиточечном шаблоне
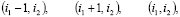

Схему (4) часто называют схемой крест. Если 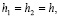 т.е. сетки по
т.е. сетки по 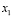 и
и 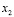 совпадают, то сетку
совпадают, то сетку 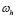 называют квадратной. На такой сетке разностную схему (4) можно записать в виде
называют квадратной. На такой сетке разностную схему (4) можно записать в виде
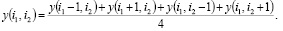
Для однородного уравнения 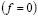 получаем
получаем
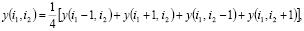
т.е. значение в центре шаблона определяется как среднее арифметическое значений в остальных узлах шаблона[3],[4],[5].
Пусть 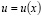 – решение задачи Дирихле (1), (2), а
– решение задачи Дирихле (1), (2), а 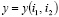 – решение разностной задачи (4), (5). Рассмотрим погрешность
– решение разностной задачи (4), (5). Рассмотрим погрешность
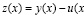 ),
), 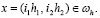
Подставляя 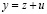 в (4), (5), получаем для погрешности
в (4), (5), получаем для погрешности 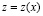 неоднородное уравнение
неоднородное уравнение
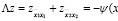 ),
),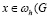 ) (6)
) (6)
с однородным краевым условием
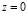 при
при 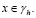 (7)
(7)
здесь
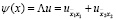 (8)
(8)
есть невязка или погрешность аппроксимации для схемы (4) на решении 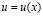 уравнения (1).
уравнения (1).
Покажем, что
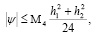 (9)
(9)
где
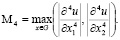
В самом деле, учитывая формулы
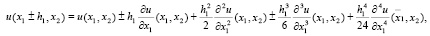
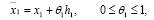
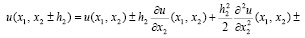
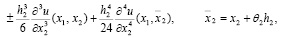
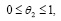
находим
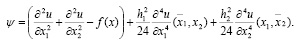
Отсюда и из (1) следует (9).
Таким образом, схема (4) имеет второй порядок аппроксимации.
Рассмотрим на примере следующую задачу:
Найти непрерывную функцию и(х, у), удовлетворяющую внутри прямоугольной
области Ω = {( 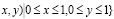
уравнению Лапласа
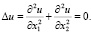
и принимающую на границе области W заданные значения, т. е.
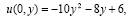
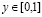 ,
,
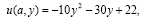
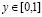 ,
,
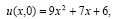
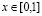 ,
,
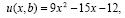
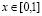 ,
,
Для ее решение составлена программа вычисление алгоритма метода сеток. Полученный численный расчет проанализированны и поведение решение показано на рисунке.
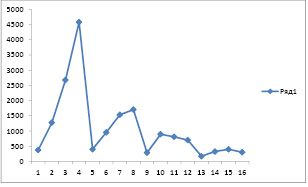
Поведение решение
Заключение
Понятие аппроксимации, устойчивости и сходимости создали необходимую базу широкого поиска эффективных разностных схем для решения задач математической физики. Алгоритмы решения задач с помощью конечно-разностных методов, представляют собой сочетание методов построения разностных аналогов задач и методов их решения. Поэтому прогресс в теории конечно-разностных методов обязан взаимосогласованному развитию этих направлении исследовании.
Библиографическая ссылка
Жунусова Л.Х., Тойганбаева Н.А. ИСПОЛЬЗОВАНИЕ МЕТОДА СЕТОК ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ УРАВНЕНИЯ ЛАПЛАСА // Успехи современного естествознания. – 2015. – № 1-1. – С. 76-79;URL: https://natural-sciences.ru/ru/article/view?id=34781 (дата обращения: 26.04.2024).



