Рассмотрим абсолютно упругое столкновение двух шаров одинаковой массы. Будем рассматривать процессы при малых скоростях, чтобы не учитывать релятивистскую зависимость массы от скорости. Массы шаров А и В обозначим соответственно m0 и m, причем m0=m. Разные обозначения вводим для того, чтобы различать, что относится к действующему шару, а что к воспринимающему действие. Вначале рассмотрим случай, когда шар В покоится относительно наблюдателя, его скорость v=0, а шар А движется со скоростью v0 в сторону шара В так, что произойдёт лобовой удар. После столкновения весь импульс шара А перейдёт к шару В, иначе говоря, шары обменяются скоростями. По закону сохранения импульса имеем: m0v0+m .0 =mv0+m0.0. Отданный и полученный импульсы будут равны m0v0-m0.0=mv0-m.0 Рассмотрим отношение импульса, полученного шаром В, к импульсу шара А, который он имел до взаимодействия, относительно наблюдателя. Назовём это отношение коэффициентом передачи импульса и обозначим k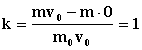 
, т.к. m0=m и v=0. Заметим, что k=1 при условии, что v=0, т.е. шар В до взаимодействия относительно наблюдателя покоился.
Рассмотрим это же взаимодействие шаров для случая, когда наблюдатель относительно системы шаров движется со скоростью -v, при этом получим, что скорость шара В будет равна v, а шара А увеличится на v, но обозначим её также v0.
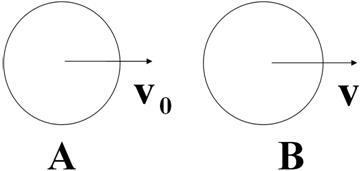
Рис. 1. Схема движения шаров
Взаимодействие шаров не изменится, они обменяются скоростями. Импульс, отданный шаром А, будет равен импульсу, полученному шаром В, m0v0-m0v =mv0-mv. Коэффициент передачи импульса будет:
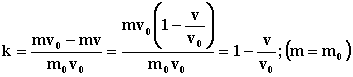
Если наблюдатель, который движется относительно системы шаров, примет постулат, согласно которому скорость шара А относительно шара В будет равна v0 независимо от скорости шара В и импульс шару В будет передаваться также как и при v=0. Получим:
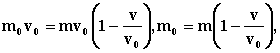
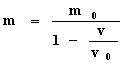
отсюда при v=0 m=m0, при 
m 
.
Обратимся теперь к взаимодействию с высокими скоростями. Пусть на частицу действует электромагнитная волна. Примем массу частицы равной массе кванта волны. Рассмотрим случай, когда скорость частицы v перпендикулярна направлению на источник волн. В этом случае применим вывод о поперечном эффекте Доплера. Если источник излучает волны частотой ν0 частица будет принимать волны частотой
.
Помножим эти частоты на 
, где h-постоянная Планка, а с - скорость света, и получим импульс излучаемой волны и импульс волны, принимаемой частицей, а, значит, и импульс, получаемый частицей
и 
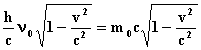
Отношение импульсов даст коэффициент передачи импульса
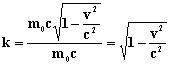
k=1 при v=0 и только в этом случае весь импульс волны, излучаемой источником, будет получен частицей.
При 
импульс волны будет лишь частично передаваться частице. Закон сохранения импульса требует знака равенства при обмене импульсами. Общепринятое мнение о том, что квант волны при определённых условиях есть частица фотон, который является неделимым и не может отдавать часть своего импульса, требует, чтобы импульс кванта излучаемой волны был равен импульсу поглощенного кванта. При рассмотрении поперечного эффекта Доплера мы получили отношение составляющей скорости света, направленной на источник света, к скорости света
.
После его преобразования
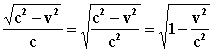
получили коэффициент передачи импульса k. Значит, коэффициент передачи импульса есть отношение скоростей. Но признанный постулат о постоянстве скорости света запрещает это. Остаётся одно - перенести этот коэффициент в равенстве импульсов к другой величине. Импульс кванта излучаемой v волны не подлежит сомнению, т.к. он может быть измерен через частоту, излучаемых источником волн. Скорость волны постоянная величина, скорость частицы v также существует, если частица движется. Остаётся только масса частицы. Обозначим её через m и запишем равенство импульсов,
сократим на с и получим [1] [с.183]
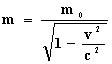
У нас получилась релятивистская формула зависимости массы тела от его скорости. Теперь проведём те же рассуждения, но используя уже прямой эффект Доплера. Частица массой m, равной массе кванта электромагнитной волны m0, движется вдоль направления, по которому, распространяется волна, например, удаляясь от источника волн. Применим выводы о частоте волны при прямом эффекте Доплера. Источник излучает волну частотой ν0, а частица принимает эту же волну частотой
.
Умножаем эти частоты на 
и получаем импульсы излучаемой волны
и 
принимаемый частицей. Определяем коэффициент передачи импульса
.
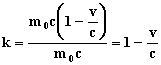Снова в угоду закону сохранения импульса, принятому мнению о неделимости кванта - фотона и постулату о постоянстве скорости света записываем равенство
,
откуда
,
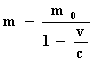получили зависимость массы от скорости.
Как в случае взаимодействия шаров, так и в случае, вытекающем из прямого эффекта Доплера, коэффициент передачи импульса содержит скорость v в первой степени, следовательно изменение направления скорости на противоположное, т.е. замену v на -v, вызовет характер изменения массы от скорости. Для массы получаем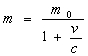 
. Это означает, что при встречном движении источника и частицы, принимающей свет, её масса будет уменьшаться.
Используем метод уравнивания импульсов излучаемого и поглощаемого квантов для получения зависимости постоянной Планка от относительной скорости источника и приёмника квантов. Выразим импульсы излучаемого и поглощаемого квантов через постоянную Планка h и частоту v. Пусть импульс излучаемого кванта будет: 
поглощаемого, исходя из эффекта Доплера, для поперечного
и
для продольного.
Приравнивая излучаемый и поглощаемый импульсы, получаем соответственно:
.
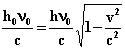
После сокращения имеем:
h0=h. 
или
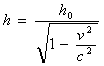
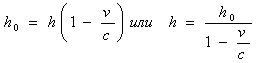
Получили зависимость h(v) такую же, как и m(v). Теперь рассмотрим зависимость расстояния от скорости. Распространение света будем рассматривать как поток равномерно движущихся фотонов. Допустим, что наблюдатель-приёмник принимает свет от трёх источников, один из которых покоится относительно наблюдателя, другой удаляется от него со скоростью v, а третий - движется перпендикулярно направлению на наблюдателя. Согласно выводам к эффекту Доплера скорости испускаемых ими фотонов относительно наблюдателя будут с; c-v и 
.
Наблюдатель решил определить длины путей, пройденных относительно него фотонами от этих источников, за время 
, измеренное по его часам, и получит соответственно: 
.
Выразим отношения l1 и l2 к l0
и 
.
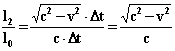Получили, что пути, пройденные фотонами за время Δt, пропорциональны их скоростям относительно наблюдателя. Из полученных равенств получаем:
и 
.
При v=0 фотоны от всех трёх источников относительно наблюдателя будут иметь скорость, равную с, и за время Δt пройдут расстояние l1=l2=l0. При v=c фотоны от второго и третьего источников относительно наблюдателя будут иметь скорость равную 0 и за то же время пройдут расстояние l1=l2=0.
Если принять постулат о постоянстве скорости фотонов относительно наблюдателя равной с, то отношение скоростей будет равно 1 и влиять на изменение значений l1 и l2 не может. В этом случае приходится признать, что уменьшение длины с увеличением v вызвано сокращением пространства в направлении движения. Для выяснения зависимости времени от скорости сравним время прохождения фотонами от тех же трёх источников одного и того же расстояния l.
;
Найдём отношение Δt1 и Δt2 к Δt0
и 
.
Из этих отношений следует, что время прохождения расстояния l обратно пропорционально скорости. В полученных уравнениях коэффициенты пропорциональности между Δt1, Δt2 и Δt0 есть отношение скоростей, из которых одна постоянная, а другая зависит от v. При v=0 коэффициент равен 1 и Δt1=Δt2=Δt0. При увеличении v переменные скорости уменьшаются, и соответственно увеличивается время прохождения расстояния l. При v=c эти скорости будут равны 0, и время для прохождения l окажется бесконечностью, т.е. фотоны от второго и третьего источников не будут приближаться к наблюдателю. Если принять постулат о постоянстве скорости фотонов, то отношение скоростей всегда будет равно 1, а коэффициент пропорциональности уже не будет отражать изменение скорости.
Ему приписано отражать изменение хода времени. При увеличении v наблюдатель обнаружит увеличение времени на прохождение участка l, а при v=c это время будет бесконечностью, т.е. фотон никогда не преодолеет расстояние l. Для самих же фотонов время будет определяться по пройденному расстоянию l1 и l2 и постулируемой скорости с.
;
;
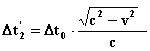При увеличении v для фотонов от второго и третьего источников ход времени будет замедляться.
Если в уравнениях для второго источника знак v поменять на противоположный, то выводы из уравнений изменятся на противоположные (относительно пространства и времени).
Следует отметить, что v - это относительная скорость источника и приёмника фотонов.
Рассматриваемое в статье движение фотонов связано с тем, что в уравнениях релятивистской механики, касающихся зависимости массы, пространства и времени от скорости, присутствует скорость света с, а это скорость фотонов.
В заключении отметим, что выводы из полученных уравнений объясняются с позиций и релятивистской и классической механик, но последняя не требует изменений массы, пространства и хода времени.
СПИСОК ЛИТЕРАТУРЫ:
-
Зисман Г.А., Тодес О.М. Курс общей физики. Т.3. - М.:«Наука», 1972.
Библиографическая ссылка
Юшкевич Р.С., Дегтярева Е.Р. О ВЗАИМОДЕЙСТВИИ ДВИЖУЩИХСЯ ТЕЛ // Успехи современного естествознания. – 2008. – № 10. – С. 7-12;URL: https://natural-sciences.ru/ru/article/view?id=10686 (дата обращения: 23.11.2024).