- Исследовать условия образования комплексов вакансий различного типа в зависимости от расстояния между ними (номер координационной сферы) для твердого раствора Ni3Al.
- Исследовать условия образования комплексов вакансий различного типа в зависимости от расстояния между ними (номер координационной сферы) для твердого раствора Ni3Fe.
- Исследовать условия образования комплексов вакансий различного типа в зависимости от расстояния между ними (номер координационной сферы) для твердого раствора Cu3Au.
- Изучение изменений энергии системы при наличии вакансионных комплексов различного типа и различной конфигурации.
Приведенные выше задания не исчерпывают возможностей программы.
Рассмотрим порядок выполнения одного из таких заданий:
Исследовать условия образования комплексов вакансий различного типа для твердого раствора Cu3Au.
Порядок выполнения:
1.Запустить программу smvtr.exe.
2.Выбрать твердый раствор ( Ni3Al, Ni3Fe, Cu3Au).
3.Задать размеры расчетной ячейки. Для этого необходимо задать число атомов в рядах ячейки по осям X и Y (рекомендуется примерно 24´24) (минимальное значение по осям X и Y - 12, максимальное - 100).
4.Задать число вакансий в окне "Число вакансий" (минимальное значение - 0, максимальное - 2).
5.Если число вакансий будет равно 2, то необходимо задать расстояние между вакансиями, равное радиусу координационной сферы (минимальное значение - 1, максимальное - 5).
6.Если есть вакансии, тогда необходимо выбрать тип вакансий из списка (Ni, Al, Fe, Cu, Au, или их комплексы-Ni-Ni, Al-Al, Fe-Fe, Ni-Al, Cu-Au, Ni-Fe). Если нет конфигурации с соответствующей сортам атомов и заданному расстоянию, то выдается сообщения об ошибке. Например, в сплаве Ni3Al возможна конфигурация с дивакансией типа Al-Al только на расстоянии, равном третьей координационной сферы.
7. Для ввода данных нажать кнопку "Установить параметры".
8. Запуск эксперимента осуществляется нажатием кнопки "Пуск". В результате расчета можно получить значение полной энергии системы.
9. Задавая различные расстояния между вакансиями и повторяя пункты 4-7 получить значение энергии системы в зависимости от количества вакансий и расстояния между ними. Записать полученные значения в таблицу.
10. Вычислить значение энергии «разорванных» межатомных связей для атома сорта A (или сорта B):
![]()
11. Найти значения энергии образования вакансии сорта А (или сорта B)![]() соответственно равна разности энергий кристалла, содержащего вакансию типа A
соответственно равна разности энергий кристалла, содержащего вакансию типа A ![]() , и идеального кристалла
, и идеального кристалла ![]() , за вычетом половины энергии связей, восстановившихся на поверхности кристалла:
, за вычетом половины энергии связей, восстановившихся на поверхности кристалла:
![]() .
.
Энергией образования вакансии называется разность энергий кристалла, содержащего заданное число N атомов и одну вакансию, и бездефектного кристалла, содержащего то же количество атомов.
12. Вычислить значения энергии образования дивакансии типа AB ![]() соответственно равна разности энергий кристалла, содержащего вакансию, и идеального кристалла, за вычетом половины энергии связей, восстановившихся на поверхности кристалла:
соответственно равна разности энергий кристалла, содержащего вакансию, и идеального кристалла, за вычетом половины энергии связей, восстановившихся на поверхности кристалла:
![]() .
.
13. Вычислить значения энергии связи двух одиночных вакансий в дивакансию 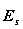 :
:
![]() .
.
14. Построить график изменения энергии связи двух одиночных вакансий в комплекс в зависимости от расстояния между вакансиями. Для обработки компьютерного эксперимента использовать электронные таблицы или среду MathCad.
15. Сравнить полученное значение со справочным.
Таблица 1. Результаты эксперимента (Система Cu3Au)
|
тип вакансий |
число вакансий m |
E0, эВ энергия идеального кристалла |
E, эВ Энергия системы |
E1, эВ энергия разорванных связей |
E2 эВ энергия образования |
E3, эВ энергия связи |
Расстояние между вакансиями n |
|
Cu |
0 |
-823,829 |
|
|
|
|
0 |
|
|
1 |
|
-821,041 |
2,788 |
1,394 |
|
0 |
|
Au |
1 |
|
-820,747 |
3,082 |
1,541 |
|
0 |
|
Au-Au |
2 |
|
-817,694 |
|
3,053 |
-0,118 |
3 |
|
Cu-Au |
2 |
|
-818,369 |
|
2,525 |
0,41 |
1 |
|
|
|
|
-818,03 |
|
2,864 |
0,071 |
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
-817,962 |
|
2,932 |
0,003 |
4 |
|
|
|
|
-817,961 |
|
2,933 |
0,002 |
5 |
|
Cu-Cu |
2 |
|
-818,61 |
|
2,431 |
0,504 |
1 |
|
|
|
|
-818,311 |
|
2,436 |
0,499 |
2 |
|
|
|
|
-818,277 |
|
2,764 |
0,171 |
3 |
|
|
|
|
-818,257 |
|
2,784 |
0,151 |
4 |
|
|
|
|
-818,254 |
|
2,787 |
0,148 |
5 |
|
|
|
|
|
|
|
|
|
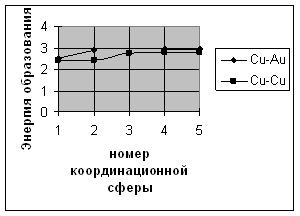
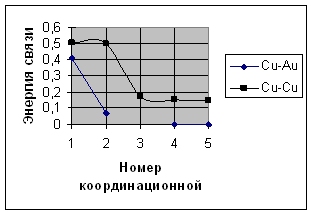
а) б)
Рисунок 1. а) Энергия образования комплексов вакансий в зависимости от расстояния между вакансиями;
б) Энергия связи в зависимости от расстояния между вакансиями.
СПИСОК ЛИТЕРАТУРЫ
- Суппес В.Г., Полетаев Г.М. Компьютерный лабораторный практикум по молекулярной физике. Ж."Физическое образование в вузах" Издательский дом МФО 2003г., Т.9, №2, с.113-124.
- Суппес В.Г., Полетаев Г.М. Компьютерный лабораторный практикум по молекулярной физике. Сб. науч. трудов "Проблемы учебного физического эксперимента" МММ., ИОСО РАО 2003, с.80-82.
- Суппес В.Г. О компьютерном лабораторном практикуме. Межвузовский сборник научных статей под редакцией В.П.Горшенина, И.В.Резанович. Профессиональное мастерство: становление, формирование и развитие. Челябинск, Издательство ЮУрГУ, 2003, С.172-178.
- Суппес В.Г., Старостенков М.Д., Дудник Е. А. О направлениях обучения с исполь- зованием компьютеров. Ж."Физическое образование в вузах" Издательский дом МФО 2004г., Т.10, №2, с.76-83.
Библиографическая ссылка
Суппес В.Г. ИССЛЕДОВАНИЕ УСЛОВИЙ ОБРАЗОВАНИЯ КОМПЛЕКСОВ ВАКАНСИЙ В ДВУМЕРНЫХ ТВЕРДЫХ РАСТВОРАХ НА КОМПЬЮТЕРНОЙ МОДЕЛИ // Успехи современного естествознания. – 2005. – № 2. – С. 33-34;URL: https://natural-sciences.ru/ru/article/view?id=7984 (дата обращения: 25.04.2024).



