Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сергиенко Л.С. 1 Куницын А.Г. 1

---

1 ГОУ ВПО «Национальный исследовательский Иркутский государственный технический университет»

Общее или временное уравнение Шрёдингера является математическим выражением дуального свойства корпускулярно-волновой природы микрочастиц материи и играет фундаментальную роль в нерелятивистской квантовой механике [1] . Если величина потенциальной энергии поля постоянна, то математическая зависимость между количественными характеристиками векторного поля не будет содержать производных по времени, и динамическая модель Шрёдингера станет стационарной. К такому уравнению приходят, например, при исследовании процесса квантования энергии гармонического осциллятора, ротатора со свободной осью, в спектральной теории атомов при изучении движения электронов в кулоновом поле ядра и др. [2]. В представленной работе рассматривается эллиптическое уравнение, являющееся модификацией стационарного уравнения Шрёдингера. Доказывается существование и единственность решения задачи Дирихле в круге для линейного дифференциального уравнения второго порядка с особой точкой в центре области исследования. Основным результатом является построение специальных функций – кратных многочленов треугольного вида, применяемых при вычислении коэффициентов ряда, представляющего решение.

Статья в формате PDF

2593 KB

уравнение

задача

решение

формула

ряд

многочлен

1. Математическая физика. Энциклопедия / Гл. ред. Л.Д. Фадеев. – М: Большая Российская энциклопедия, 1998. – 691 С.

2. Тихонов А.Н., Самарский А.А. Уравнения математической физики: учеб. пособие. – М: Наука, 1977. 735 С.

3. Полянин А.Д. Справочник по линейным уравнениям математической физики. – М.: ФИЗМАТЛИТ, 2001. – 576 С.

4. Сергиенко Л.С. Математическое моделирование физико-технических процессов. – Иркутск: Изд-во Ир ГТУ, 2006. – 228 c.

5. Сергиенко Л.С., Баенхаева А. В. О задаче Дирихле для одного класса вырождающихся на оси эллиптических уравнений // Современные методы теории функций и смежные проблемы: материалы Воронежской зимней математической школы / Воронежский государственный университет, Московский государственный университет им. М. В. Ломоносова, Математический институт им. В. А. Стеклова РАН. – Воронеж: Издательско – полиграфический центр Воронежского государственного университета, 2011. – 374 с.

6. Сергиенко Л.С., Баенхаева А. В. Первая краевая задача для стационарного уравнения класса Шрёдингера // Вестник Ир ГТУ / научный журнал – Иркутск: Изд-во Ир ГТУ, 2011 – № 10, выпуск 1 (48) -342 с.

7. Sergiyenko L.S., Nesmeyanov A.A. On evolution of stationary processes near the origins of excitation // International journal of applied and fundamental research. – №1, 2012. – 54 c.

Постановка задачи

Рассмотрим стационарное уравнение Шрёдингера с двумя независимыми переменными, которое формально, отвлекаясь от физического смысла аргументов, можно записать в следующем виде [3]

В частных случаях при

для последнего уравнения найдены корректные постановки краевых задач в определённых условиях [4–5].

В представленной работе исследуется Задача. В области

найти решение уравнения

(1)

удовлетворяющее граничному условию

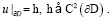(2)

Замечание 1. В дальнейшем для упрощения выкладок будем считать радиус круга единицей масштаба рассматриваемой системы координат: R=1.

Разделение переменных по методу Фурье

Нетривиальное решение граничной задачи 1 будем искать в полярных координатах в виде

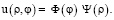(3)

В результате подстановки произведения (3) в уравнение (1) и разделения переменных с постоянной λ получается уравнение для функции

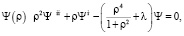(4)

и задача на собственные значения для функции

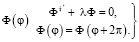(5)

Общее решение однородного линейного уравнения (5) определяется с помощью характеристического уравнения в виде суперпозиции гармоник

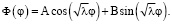
Для того, чтобы Ф была однозначной периодической функцией, должно выполняться

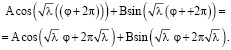
Выбирая собственные значения 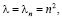получаем

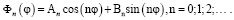(6)

При каждом фиксированном n из (4) получаем

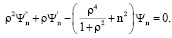. (7)

Так как уравнение (7) при любом заданном 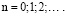имеет особую точку при 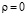, его решение будет иметь вид степенного ряда, начинающегося с :

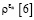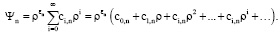(8)

Значения характеристического показателя 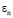и коэффициентов 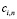можно определить подстановкой ряда (8) в уравнение (7). Последовательно приравнивая к нулю коэффициенты при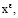 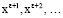получаем систему следующих уравнений

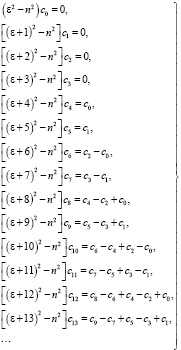
Считая 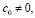из первого уравнения находим 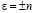. Чтобы найти сингулярное ограниченное при 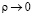решение уравнения (7), полагаем 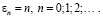Тогда из последней системы заключаем, что 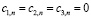. В этом случае все последующие нечётные коэффициенты 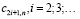также должны быть равны нулю, а все чётные коэффициенты определятся через сумму предыдущих по альтернативным формулам

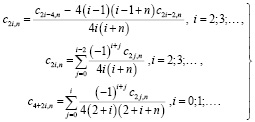(9)

Последовательное применение формулы (9) при 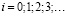позволяет получить выражение

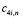через ,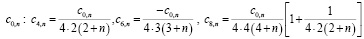

,

. . .

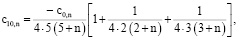
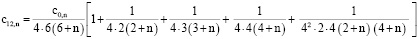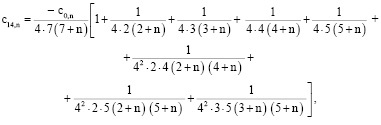
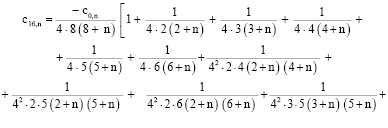
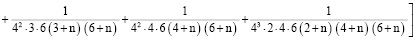
При 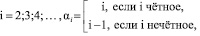или

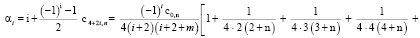
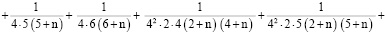
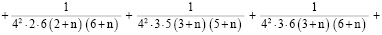
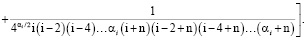(10)

Обозначим специальные вспомогательные функции

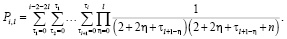(11)

Полагая 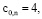уравнения системы (10) при 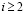можно записать в виде

,

,

. . .

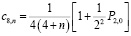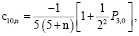
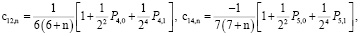
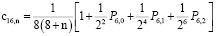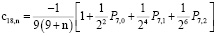
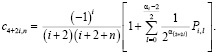(12)

Пример вычисления коэффициентов ряда (8).

По формулам (11) – (12) найти коэффициенты ряда (8): а) 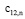и в)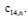

Решение. а)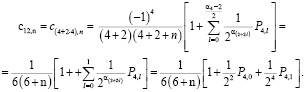

Найдём значение коэффициента :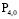

.

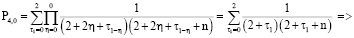
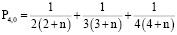Определим .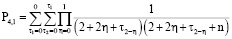

Так как

,

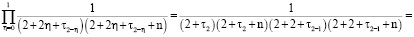
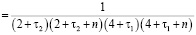имеем

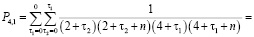
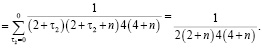
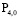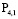Подставляя и в формулу

,

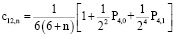получим

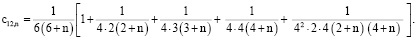
в)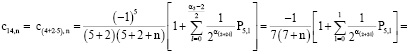

.

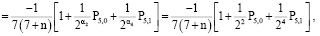
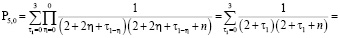
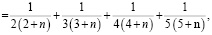
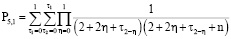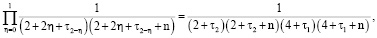
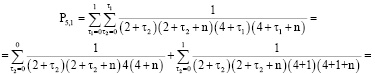
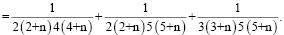
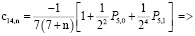
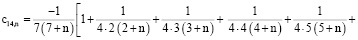
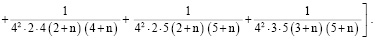
Алгоритм вычисления коэффициентов

Для простоты алгоритм вычисления коэффициентов ряда

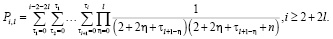
рассмотрим на примере составления кратных сумм вида

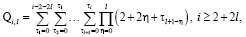
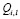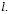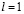Определим сначала последовательности сумм c одинаковым индексом При получаем

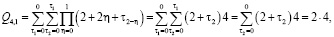
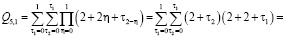
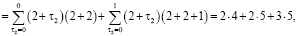
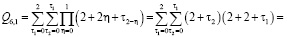
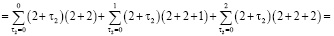
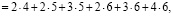
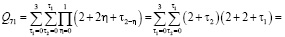
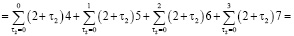
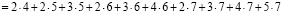и т.д.

Последовательности множителей в слагаемых рассмотренных сумм 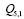, 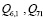можно легко составить с помощью треугольных матриц

, ,

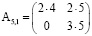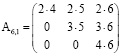Так как этим свойством обладают все выражения 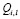, назовём их кратными многочленами треугольного вида, а функции 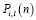, представляющие их модификацию соответственно кратными суммами треугольного вида.

Решение краевой задачи 1. Объединяя полученные результаты, определим решение задачи (1) – (2) в полярных координатах

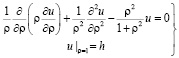(13)

по формуле (3): 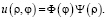Выше было доказано, что после разделения переменных задачи (13) получаем два уравнения, первое из которых 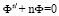имеет частные решения (6)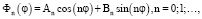

При каждом фиксированном n второе уравнение

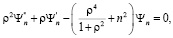
имеет частные решения вида (8)

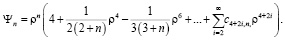
Коэффициенты степенного ряда (8) определяются по формулам (12)

,

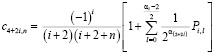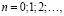
в которых

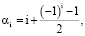
а кратные многочлены 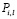заданы соотношениями (11)

.

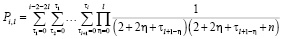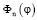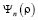Подставляя выражения и в формулу (3), определяем две системы собственных функци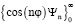й и 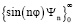, которым соответствуют частные решения первого уравнения (13)

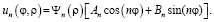
Суперпозиция всех этих решений

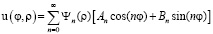(14)

также будет решением этого уравнения. Коэффициенты 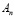и 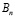определяются из граничного условия (13)

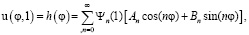(15)

если функцию 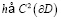разложить в абсолютно и равномерно сходящийся тригонометрический ряд Фурье

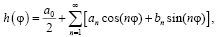(16)

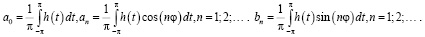
Сравнивая ряды (15) и (16), получаем

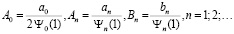(17)

Применимость принципа суперпозиции

Сходимость построенных рядов, возможность их дифференцирования в круге , а также непрерывность функции 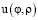на границе этого круга доказываются классическими методами [2, с. 308–310].

С помощью альтернирующего метода Шварца построенное решение может быть продолжено за пределы круга в области более общего вида [1].

Библиографическая ссылка