Неисчислимый моральный и огромный материальный ущерб приносят ураганы. Особенно в прибрежных районах тропического и субтропического пояса. Тропические ураганы и циклоны (ТЦ) зарождаются в открытом океане. В зоне своего влияния они кардинально трансформируют структуру верхнего слоя океана. В свою очередь, температура поверхности воды и теплозапас верхнего слоя определяют мощность и траекторию движения ТЦ.
Разработанная в [2, 4] модель используется для изучения формирования вертикальной термогидродинамической структуры верхнего слоя океана в районе буя ЕВ-10 во время прохождения урагана Элоиза 21–27 сентября 1975 года [5]. Модель описывает изменения вертикального распределения средних значений характеристик стратифицированной среды и параметров мелкомасштабной турбулентности в приближении горизонтальной однородности нелинейной системой одномерных дифференциальных уравнений гидродинамики, записанных без учета адвекции и горизонтального турбулентного обмена в виде
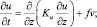 (1)
(1)
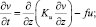 (2)
(2)
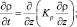 (3)
(3)
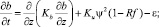 (4)
(4)
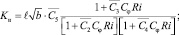 (5)
(5)
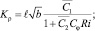 (6)
(6)
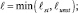 (7)
(7)
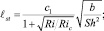
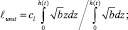 (8)
(8)
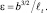 (9)
(9)
Здесь u, v – компоненты вектора скорости течения; ρ – плотность, как функция температуры и солености морской воды; b – энергия турбулентности; ε – скорость вязкой диссипации; t – время; z – вертикальная координата, направленная от поверхности вглубь океана. Ri – градиентное число Ричардсона 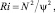 где N2 – частота Вяйясяля – Брента
где N2 – частота Вяйясяля – Брента 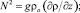 y2 – квадрат вертикального сдвига скорости
y2 – квадрат вертикального сдвига скорости 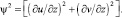
В уравнение (7) входит масштаб турбулентности l, который определен по комбинированной гипотезе (8) [2]. Скорость вязкой диссипации (9) определяется из гипотезы Колмогорова.
При моделировании турбулентных слоев трения особенно важно правильное и по возможности полное описание процессов вертикального турбулентного обмена с учетом стратификации морской воды, поскольку он является одним из основных механизмов быстрой перестройки верхнего слоя океана во время прохождения шторма. Выражения для вторых моментов компонентов скорости и плотности, выписанные в локально-равновесном приближении стратифицированного горизонтально-однородного течения (2), представляют собой гипотезу Буссинеска и в соответствии с К-замыканиями позволяют определить коэффициенты вертикального турбулентного обмена Ku и Kρ в виде (5, 6). Для коэффициента турбулентного обмена Kb примем Kb = cbKu Из-за отсутствия данных наблюдений считаем, что cb = 0,73.
Краевая задача решается при следующих начальных и граничных условиях:
t = 0; u = u°(z); v = v°(z);
ρ = ρ°(z); b = b°(z);
z = 0; 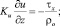
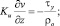
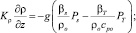
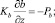
z = H; u = v = 0;
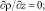
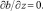 (10)
(10)
Здесь τx, τy – составляющие касательного напряжения ветра на верхней границе водоема; PT, Ps, Pb – потоки тепла, соли и энергии турбулентности из атмосферы в водную среду, ρo, сpo – характерное значение плотности и удельная теплоемкость жидкой среды; βT, βs – коэффициенты термического расширения и соленосного сжатия морской воды, H – глубина водоема. Для решения нестационарной задачи все потоки на верхней границе рассчитываются по стандартным методикам, приведенным в работе [1].
В силу нелинейности задача (1)–(4) с замыканиями (5)–(9) и краевыми условиями (10) решается численно конечно-разностными методами, для которых пока не существует общей теории сходимости приближенного решения к точному. Это требование удовлетворяется при использовании абсолютно устойчивых консервативных численных схем с высоким порядком аппроксимации производных по пространственной координате и времени.
Уравнения для плотности ρ и составляющих вектора скорости течения u, u рассчитывались хорошо зарекомендовавшим себя способом прогонки [3]. Сведение исходных уравнений к трехточечной схеме осуществляется бокс-методом, позволяющим искать решение в классе разрывных и высокоградиентных функций. Нелинейность диффузионных слагаемых из-за переменных коэффициентов вертикального турбулентного обмена вынуждает проводить их квазилинеаризацию путем явного задания значений коэффициентов из предыдущего шага. Возникающие вследствие этого погрешности численного решения могут быть компенсированы итерационным установлением с заданной точностью по всем коэффициентам вертикального турбулентного обмена.
Для интегрирования уравнений по времени используется схема второго порядка точности Кранка – Николсона:
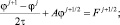
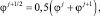 (11)
(11)
где φ = {u, u, ρ} – искомая функция; 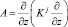 – конечно-разностный оператор диффузии; 2τ – шаг по времени, j = 1, ...; J – индекс аппроксимации по времени; F – правая часть конечно-разностного аналога.
– конечно-разностный оператор диффузии; 2τ – шаг по времени, j = 1, ...; J – индекс аппроксимации по времени; F – правая часть конечно-разностного аналога.
После аппроксимации (11) по пространственной координате бокс-методом для функции φk, определенной в узлах сдвинутой сетки, получим трехточечное выражение
 (12)
(12)
Коэффициенты трехточечной схемы равны
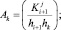
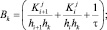
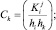
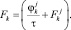 (13)
(13)
Исходя из тех же принципов разработки конечно-разностных аналогов аппроксимируем уравнение баланса энергии турбулентности (4).
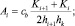
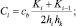
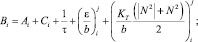
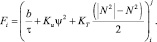 (14)
(14)
Конечно-разностная задача (11)–(14) решается методом прогонки. При этом по рекуррентным формулам
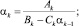
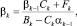 k = 2, 3, ..., N – 2; (15)
k = 2, 3, ..., N – 2; (15)
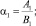
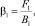 k = 1 (16)
k = 1 (16)
находятся коэффициенты ak, bk, а обратной прогонкой рассчитываются значения 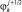 :
:
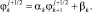 (17)
(17)
Краевые условия на одной из границ задаются в виде потока Pφ для физической величины φ. Все потоки рассчитываются с дискретностью стандартных наблюдений метеоряда с шагом 1 или 3 часа, что создает затруднения при обеспечении краевых условий необходимыми потоками с регулярностью несколько секунд в соответствии с установленным временным шагом τ решения задачи. Это достигается интерполяцией данных метеонаблюдений в требуемые моменты времени. При вычислениях используется линейная интерполяция и интерполяция сплайнами.
Анализ теплового баланса показывает, что с 21 по 27 сентября общие потери тепла океаном составили значительную величину 13440 Дж•см–2. Столь большое выхолаживание произошло за счет интенсивного испарения с поверхности океана первоначально под действием ураганного ветра, а впоследствии за счет вторжения в след урагана холодного сухого воздуха с северо-запада. Потери тепла максимальны в период сильных ветров и составляют 297 Дж•см–2•сут–1. До прохождения ТЦ (0–36 ч) скорость ветра в среднем была 10 м/с. Во время урагана (36–60 ч) ветер усилился до 35 м/с и сменил направление на противоположное. К концу третьих суток установившаяся скорость ветра равнялась 8 м/с (72–120 ч). Такие изменения внешних условий привели к перестройке термической структуры ВСО (рис. 1).
За первые 36 часов толщина изотермического слоя увеличилась на 5 м, а температура понизилась на 0,25 °С. В последующие сутки толщина квазиоднородного слоя составила 55 м, то есть возросла вдвое при понижении температуры на 1,3 °С (рис. 2).
После прохождения урагана температура продолжала незначительно падать (0,1 °С/сут) и нижняя граница термической однородности зафиксировалась на глубине 53 м. Сформировавшийся под воздействием урагана слой скачка температуры составляет 2,5 °С и носит ярко выраженный характер. Ослабление ветра, сопровождавшееся прогревом, привело к заметному размыванию слоя скачка (рис. 1).
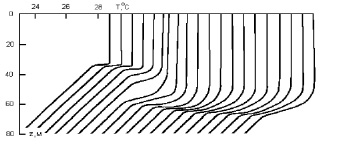
Рис. 1. Эволюция вертикальной термической структуры за период с 8 час 22.09.75 по 8 час 25.09.75 с интервалом 4 часа
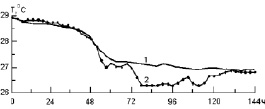
Рис. 2. Расчетная (1) и наблюдаемая (2) температура поверхности океана
После прохождения ТЦ в часы прогрева на фоне сложившейся термической структуры зафиксировано появление мелких, толщиной 15–20 м, новых термических образований с температурой примерно на 0,2 °С выше фоновой, которые легко разрушались в ночное время. Сравнение рассчитанного и наблюдаемого ходов температуры (рис. 2) показывает их хорошую согласованность в течение первых 8 часов после начала урагана. Примерно в это же время возникает не учтенный в модели апвеллинг, который дополнительно понижает температуру реального океана. Этим объясняется различие поведения теоретической и эмпирической кривых в период с 54 до 72 час от начала расчета. В дальнейшем не учтенные в модели механизмы адвективного переноса усиливались и привели к еще большему рассогласованию сравниваемых температур.
Одновременно с термической произошла резкая динамическая перестройка водных масс. Если первоначально дрейфовое течение охватывало слой толщиной 35 м и представляло собой четко выраженную спираль Экмана со скоростями, не превышающими 0,4 м/с, то под воздействием урагана скорости возросли до 1,2 м/с. Течение проникло до глубины 65–70 м, приняв инерционный характер с периодом 35 часов. При этом слой толщиной 50 метров стал двигаться с практически одинаковой скоростью, напоминая собой «плиту», ниже которой наблюдается быстрое замедление движения жидкости со средним градиентом 5•10–2 с–1. Рассчитанная в модели скорость течения в следе урагана превышает наблюдаемые на горизонте 50 м значения на 15 %. Это связано с тем, что в естественных условиях в океане под воздействием ТЦ наблюдается подъем холодных вод – апвеллинг, ведущий к увеличению доступной потенциальной энергии ВСО за счет уменьшения кинетической энергии и тем самым к снижению скорости течения.
Вертикальная турбулентная структура определяется энергией турбулентности. Динамическое уравнение (4) описывает её изменения за счет неустойчивости вертикальных градиентов скорости осредненного течения и за счет изменения потенциальной энергии стратификации среды. Анализ общей картины поведения турбулентных характеристик во время шторма показывает, что тангенциальное напряжение ветра является основным источником их изменений. Турбулентность ВСО в этот период определяется как обрушением поверхностных волн, учитываемым в виде потока Рb в краевом условии (11), так и сдвигом скорости дрейфового течения. Продукция вертикальных пульсаций скорости за счет потенциальной энергии неустойчивой стратификации среды во время урагана заметного влияния на турбулентность не оказывает. Увеличение всех характеристик турбулентности как у поверхности, так и во всем ВСО происходит практически одновременно с возрастанием скорости ветра.
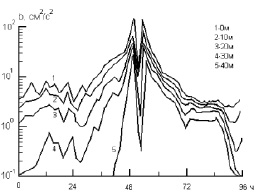
Рис. 3. Изменение энергии турбулентности в слое 0–40 м в ВСО при прохождении урагана
Максимальному ветру соответствует максимум энергии турбулентности. Вертикальная структура характеризуется её уменьшением с глубиной. Турбулентная структура ВСО до и после прохождения ТЦ заметно различается. Турбулентность в следе ТЦ испытывает большое влияние со стороны тепловых потоков на поверхности океана, которые в периоды прогрева приводят к повышению гидродинамической устойчивости водных масс и многократному уменьшению значений турбулентных характеристик в толще ВСО. Во время ночного выхолаживания поверхности океана в рассчитанной термической структуре возникает достаточно глубокий (порядка 20 м) слой положительных градиентов температуры. Это приводит к быстрому восстановлению значений турбулентных характеристик. Время релаксации турбулентности на горизонте 40 м составляет 3 часа. Особенно подвержены суточному ходу коэффициенты турбулентной вязкости и температуропроводности, характерные дневные значения которых составляют 100, а ночью могут достигать 2000 см2с–2. Столь высокие значения коэффициентов Ku и KT объясняются усилением вертикального турбулентного перемешивания, приводящего к увеличению турбулентного обмена теплом и количеством движения в ночное время в ходе конвективного выравнивания плотности.
Библиографическая ссылка
Ксенофонтов А.С., Москаленко Л.А. ФОРМИРОВАНИЕ ВЕРТИКАЛЬНОЙ СТРУКТУРЫ ВЕРХНЕГО СЛОЯ ОКЕАНА ПОД ВОЗДЕЙСТВИЕМ УРАГАНА // Успехи современного естествознания. – 2016. – № 11-1. – С. 127-131;URL: https://natural-sciences.ru/ru/article/view?id=36197 (дата обращения: 24.04.2024).



