Введение
Успехи современного естествознания требуют дальнейшего развития теории дифференциальных уравнений в частных производных, что приводит к необходимости исследования локальных и нелокальных задач для нагруженных уравнений различных типов. В последние годы появилось значительное число публикаций, проблемно ориентированных на нагруженные уравнения [4, 7, 10], где исследовались локальные и нелокальные краевые и внутреннекраевые задачи для нагруженных уравнений в частных производных гиперболического, параболического, эллиптического и смешанного типов. Следует отметить такие применения нагруженных уравнений, как метод математического моделирования нелокальных, в том числе фрактальных, процессов и явлений, и метод эффективного поиска решений дифференциальных уравнений. Математической основой физики фракталов, в особенности дробной динамики, стали нагруженные дифференциальные уравнения, демонстрирующие роль этих уравнений в различных отраслях современной науки. Актуальность исследования краевых задач для нагруженных уравнений можно обосновать как внутренними потребностями теоретического обобщения результатов, так и прикладным значениям.
Цель исследования: доказать однозначную разрешимость внутреннекраевой задачи для нагруженного уравнения третьего порядка с кратными характеристиками.
Постановка задачи. В области 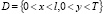 рассмотрим уравнение
рассмотрим уравнение
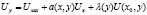 . (1)
. (1)
Задача А. Найти регулярное в области D решение уравнения (1), из класса 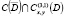 с непрерывной вплоть до x=1 производной первого порядка по x, удовлетворяющее условиям:
с непрерывной вплоть до x=1 производной первого порядка по x, удовлетворяющее условиям:
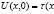 ),
), 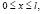 (2)
(2)
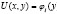 ),
), 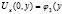 ),
), 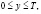 (3)
(3)
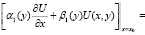
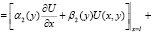
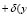 ),
), 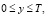 (4)
(4)
где τ(y), φ1(y), φ2(y), α1(y), α2(y), β1(y), β2(y), δ(y) – заданные функции, непрерывные в замыкании области их определения, x0 – фиксированная точка интервала 0 < x < 1 причем β2(y) ≠ 0.
Задача А относится к классу нелокальных задач, исследованием которых занимались многие авторы [1 – 6, 8].
Доказательство существования и единственности решения. Рассмотрим случай, когда 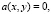 то есть уравнение
то есть уравнение
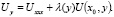 (5)
(5)
Пусть существует решение 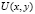 задачи (2)-(4),
задачи (2)-(4),
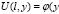 ),
), 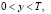 (6)
(6)
для уравнения (5).
Функция Грина задачи (2),(3),(6) для уравнения
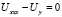 (7)
(7)
задается формулой [6, 8]:
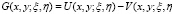 )
)
где 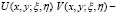 фундаментальные решения уравнения (7), которые имеют вид:
фундаментальные решения уравнения (7), которые имеют вид:
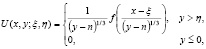
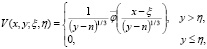
где
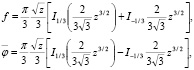
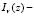 функция Бесселя, функция
функция Бесселя, функция 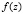 и
и 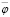 – функции Эйри и удовлетворяют уравнению [9]:
– функции Эйри и удовлетворяют уравнению [9]:
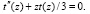
Основные свойства функций 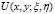 и
и 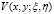 , их оценки вместе с частными производными порядка
, их оценки вместе с частными производными порядка 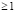 приведены в [6, 8].
приведены в [6, 8].
Из свойств функции Грина заключаем, что решение 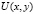 в области D представимо в виде
в области D представимо в виде
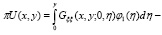
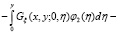
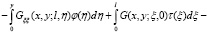
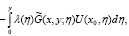
где
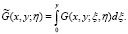
Найдем значение 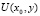 . Для этого положим
. Для этого положим 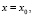 в последнем равенстве.
в последнем равенстве.
Получим:
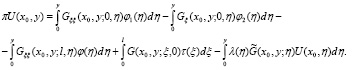 (8)
(8)
Обозначим 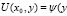 ), тогда (8) перепишется в виде:
), тогда (8) перепишется в виде:
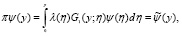 (9)
(9)
где
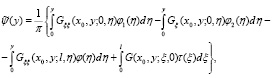 (10)
(10)
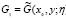 ).
).
Равенство (9) есть интегральное уравнение Вольтера второго рода, которое однозначно разрешимо.
Решение интегральное уравнения (9) можно выписать через резольвенту 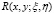 ядра
ядра 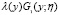 :
:
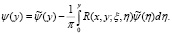 (11)
(11)
Таким образом, решение задачи (1),(2),(3), и 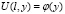 имеет вид
имеет вид
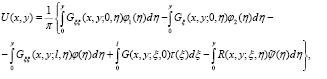 (12)
(12)
Удовлетворим краевому условию (4). Для этого из (12) найдем 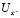 Имеем
Имеем
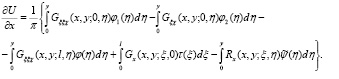 (13)
(13)
Подставим (13) в краевое условие (4). В результате получим равенство:
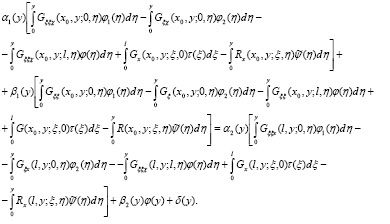 (14)
(14)
Преобразовав (14) с учетом (10), получим интегральное уравнение Вольтерра второго рода относительно функции 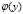
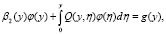 (15)
(15)
где
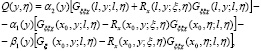
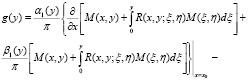
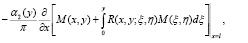
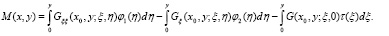
По условию 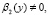 то есть (15) является интегральным уравнением Вольтерра второго рода, которое безусловно и однозначно разрешимо в классе
то есть (15) является интегральным уравнением Вольтерра второго рода, которое безусловно и однозначно разрешимо в классе 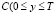 ). Обращая его через резольвенту ядра
). Обращая его через резольвенту ядра 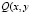 ) получим значение φ(y) то есть
) получим значение φ(y) то есть 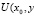 ).
).
Таким образом, решение задачи (2)-(4) и (6), существует, единственно и определяется по формуле (12).
В случае, когда 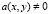 опираясь на
опираясь на
свойства функции Грина для задачи (7), (2)-(3)
и 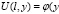 ) имеем (15)
) имеем (15)
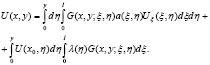
Интегрируя внутренний интеграл в первом слагаемом по частям, получим:
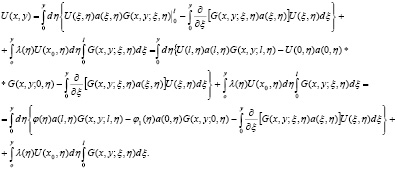 (16)
(16)
Равенство (16) перепишем в виде (17)
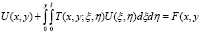 )
)
где
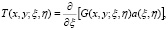
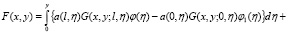
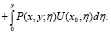
Обращая (17) через резольвенту 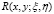 ядра
ядра 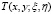 будем иметь
будем иметь
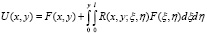
или
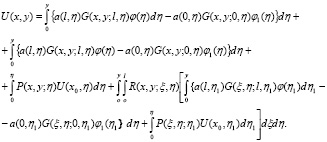 (18)
(18)
После преобразования (18), получим
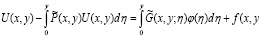 ) (19)
) (19)
где 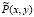 и
и 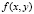 выражаются через интегралы от
выражаются через интегралы от 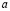 и
и 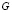 . Полагая в (18)
. Полагая в (18) 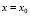 и считая пока правую часть ее известной, получим интегральное уравнение Вольтерра второго рода относительно
и считая пока правую часть ее известной, получим интегральное уравнение Вольтерра второго рода относительно 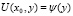
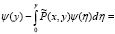
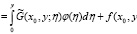 )
)
которое имеет только одно решение.
Найденное значение 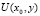 подставим в равенство (19). Удовлетворяя его граничному условию (4), снова получаем интегральное уравнение Вольтерра второго рода относительно
подставим в равенство (19). Удовлетворяя его граничному условию (4), снова получаем интегральное уравнение Вольтерра второго рода относительно 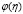 , которое однозначно разрешимо.
, которое однозначно разрешимо.
Библиографическая ссылка
Водахова В.А., Тлупова Р.Г., Шерметова М.Х. ВНУТРЕННЕКРАЕВАЯ ЗАДАЧА ДЛЯ НАГРУЖЕННОГО УРАВНЕНИЯ ТРЕТЬЕГО ПОРЯДКА С КРАТНЫМИ ХАРАКТЕРИСТИКАМИ // Успехи современного естествознания. – 2015. – № 1-1. – С. 71-75;URL: https://natural-sciences.ru/ru/article/view?id=34780 (дата обращения: 19.04.2024).



