Статья является результатом научных исследований сотрудников кафедры Прикладной математики Томского политехнического университета, работающих в коллективе научной школы «Разработка физических основ программного обеспечения энерго- информационного представления функциональных особенностей организма в задачах лечебно- профилактической медицины» и посвящена применению математических методов для прогнозирования здоровья детей. Дан краткий обзор использующихся для этих целей методов. Изложены основные этапы разработки комплексного прогноза с определением степени риска наиболее частых заболеваний у детей раннего возраста. Особое внимание уделено: разработке прогностических моделей состояния здоровья детей с использованием методов выявления: скрытых закономерностей; типов магистрального поведения организма ребенка на основе построения и анализа магистральных траекторий, определяющих для каждой однородной группы прогноз развития; исследованию видов адаптации с учетом индивидуальных особенностей.
Большое значение имеет прогностический подход в педиатрии, главной задачей которой является не только охрана жизни ребенка, но и поддержание его здоровья на высоком уровне. Ежегодно до 38 % детей рождаются больными или заболевают в период новорождённости. При этом общая заболеваемость новорождённых снизилась с 6020,6 (2006 г.) до 5396,9 (2012 г.) на 10000 новорождённых [3].
В настоящее время наибольшее число исследований в сфере биомедицинского прогнозирования посвящено исходу течения заболевания. Значительно меньше изучены вопросы прогнозирования состояния здоровых новорожденных детей при воздействии тех или иных факторов. Однако решение данных задач представляет собой наиболее актуальную часть проблемы, поскольку открывается возможность профилактики не только заболеваний, но и состояний на гране нормы и патологии, что особенно актуально для детей раннего возраста, когда малейшие изменения оказывают огромное влияние на состояние здоровья новорожденных.
В статье показан комплексный подход оценки состояния здоровья ребенка в будущем. Для решения поставленных прогностических задач предполагается использовать разработанные и реализованные авторами подходы и методы:
1) комплексного прогнозирования функционального состояния ребенка;
2) получения адаптационных характеристик на основе интегрально-информационных критериев;
3) выявления закономерностей в структуре данных.
Статистическая обработка исходных данных. Для того чтобы получить достаточно надежную оценку и прогноз здоровья детей, необходимо выбрать признаки, которые не только описывали бы состояние организма в прошлом и настоящем, но и отражали особенности его реактивности и адаптационные возможности. В качестве таких признаков авторами исследуются анамнестические данные, позволяющие выявить наследственно-генетический фон, дающие представление о действии неблагоприятных факторов во антенатальном, интра- и перинатальном периодах; данные лабораторных и инструментальных исследований (показатели крови, кариометрии, кардиоинтервалографии), позволяющие проводить оценку состояния организма ребенка и выявить взаимосвязь систем организма. Для успешного решения задачи прогнозирования на первом этапе исследований выявлены и удалены аномальные наблюдения в данных. Для решения этой задачи использовался метод Ирвина. При использовании этого метода вычисляется величина λt:
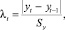
где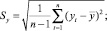 
Если полученное λt превышает табличное значение (находимое в зависимости от числа наблюдений во временном ряде и уровня значимости), то элемент yt считается аномальным наблюдением. Аномальные наблюдения необходимо исключить из временного ряда, заменив на расчетные значения (например, на среднее из двух соседних значений). Результаты для показателя «Васкулоэндотелиальный ростовой фактор VEGF» приведены на рис. 1.
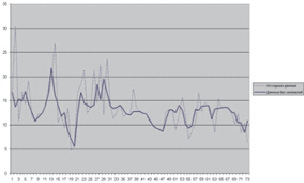
Рис. 1. Результат применения метода Ирвина на временном ряде показателя VEGF
На втором этапе исследований все полученные данные были ранжированы по информативности и степени влияния на результирующие показатели с помощью построения диаграммы Парето [4]. Основными достоинствами данного метода являются: визуальное представление результатов; хорошая достоверность выделения информативных показателей; сохранение исходных данных в неизменном виде, что ускоряет и облегчает интерпретирование полученных результатов. Согласно правилу построения диаграммы Парето, по исходным данным определяется частота отклонений каждого показателя от нормы [4]:
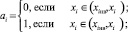
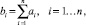
где bi – число отклонений i-го показателя; хi – значение i-го показателя конкретного пациента; (xiн, xiв) – нижняя и верхняя граница нормы i-го показателя; n – количество показателей.
Полученные отклонения располагаются в порядке их значимости и вычисляется кумулятивный процент.
Диаграмма Парето, построенная по показателям исследования, представлена на рис. 2.
Большинство решающих правил используют методы статистики, основанные на применении прогностических коэффициентов и обучающих выборок, составленных из группы детей с известным состоянием здоровья. Для формирования прогностических коэффициентов была произведена оценка степени тесноты связей: для количественных признаков с помощью выборочного коэффициента корреляции, а для качественных признаков – рангового коэффициента парной корреляции [5].
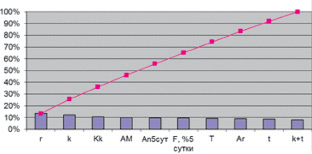
Рис. 2. Диаграмма Парето
Комплексное прогнозирование здоровья детей
Естественно-научной основой предвидения является способность организма опережающе отражать действительность, как механизм адаптации к изменяющимся условиям жизнедеятельности. Одним из принципов, который необходимо реализовать при построении математической модели прогноза состояния здоровья детей, является оценка адаптационных возможностей организма, формирование характера напряжения и декомпенсации всех систем организма, возникших в неонатальном периоде у детей с различным сроком гестации, опираясь на данные исследований.
Оценивая адаптационные возможности детей, можно установить уровень функционирования и функциональные резервы организма, выявить пограничные состояния, т.е. состояние здоровья на гране нормы и патологии (например, при слабой адаптации организм ребенка не справляется с воздействием изменяющихся факторов внутренней и внешней среды, что приводит к срыву и как следствие к заболеваниям). При этом использовался обобщенный интегральный критерий, основанный на использовании информационной меры Кульбака, в рассмотрении меры Кульбака, как меры «предпочтительности» поведения биообъекта:
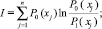
где n – количество информативных признаков; P0(хj) – вероятность, характеризующая «предпочтительную» вероятность состояния объекта, т.е. случай, когда отклонения j переменной от «нормы» равно 0. В работе при оценке адаптационных возможностей организма ребенка за «норму» («эталонное» состояние) принято считать состояние, при котором значения всех переменных равны среднестатистическим значениям (для однородных групп обследуемых).
P1(хj) – вероятность того, что значение признака хj соответствует «норме».
В качестве «предпочтительного» поведения в интегральном критерии выбираются фоновые значения показателей крови, соответствующие индивидуальной норме. Полученная интегральная мера, позволяет оценить только суммарное отклонение всех количественных признаков, измеренных однократно в некоторый момент времени. Поскольку исследования проводятся в некоторый период времени, то полученная дискретная функция рассматривается как некоторая адаптационная характеристика (адаптационная стратегия). Выделение эталонных типов функций (адаптационных стратегий) осуществлялось при помощи кластерного анализа. В результате было получено 5 эталонных типов [1].
Распределение типов адаптационных стратегий, полученных при обследовании детей, представлено в табл. 1. На рис. 3 представлен график адаптивно-компенсаторного типа адаптационной кривой.
Таблица 1
Распределение типов адаптационных стратегий в зависимости от однородной группы
|
Группа Тип кривой |
Контроль |
Сравнения |
Основная |
|
Адаптивный |
6 % |
– |
41 % |
|
Компенсированный |
40 % |
48 % |
43 % |
|
Адаптивно-компенсаторный |
13 % |
10 % |
6 % |
|
Дезадаптивный |
24 % |
40 % |
– |
|
Гиперкомпенсированный |
17 % |
2 % |
10 % |
Рис. 3. График адаптивно-компенсаторной адаптационной функции
Для прогнозирования типа адаптационной реакции организма осуществлен подбор для адаптационной функции в любой интересующий нас момент времени t, наиболее подходящего вида аппроксимирующей зависимости. С этой целью было выбрано 7 видов эмпирических зависимостей (линейная, логарифмическая, полиномиальная 2-го порядка и 3-го порядка, степенная, экспоненциальная, линейная фильтрация). Подбор функции осуществлялся на основе метода наименьших квадратов. Анализ полученных результатов эксперимента показал, что аппроксимацию построенных по интегральному критерию функций достаточно осуществлять при помощи полиномиальной функции аt2 + bt + с, производя классификацию на основе анализа значений коэффициентов a, b и c. Проверка достоверности статистической связи между типом кривой и функциональным состоянием биообъекта осуществлялась по критерию Хи-квадрат.
Использование данного подхода позволяет оценить степень отклонения текущего состояния биообъекта от «предпочтительного». Таким образом, имеем интегральную оценку адаптационных возможностей организма, которая дает возможность выявить закономерности в сложных процессах, обусловленные влиянием внешних факторов на функциональное состояние организма. При этом мы исходим из следующих положений: если измеряемые параметры изменяются случайно, причем не наблюдается никакой закономерной тенденции, то система практически не изменяет своего состояния, и информационные показатели не превышают заданного уровня. Если влияние внешней среды или условий пребывания организма приводят к изменению состояния, информационные показатели превысят принятый исходный уровень тем больше, чем сильнее изменения состояния биосистемы.
Для успешного осуществления прогноза недостаточно знать только адаптационные возможности организма ребенка, необходимо также учитывать степень напряжения всех систем организма. С этой целью осуществлена типизация магистрального поведения организма ребенка на основе построения и анализа магистральных траекторий.
Развитие динамических процессов происходит по некоторой траектории, обеспечивающей равновесное сбалансированное изменение переменных состояния во времени. Такие траектории называются магистралями. При различных начальных значениях переменных мы получим множество траекторий. Если в качестве начальных значений брать значения показателей здоровых детей, у которых степень напряжения систем организма не выходит за границы нормы, то получим множество траекторий, среди которых будут наиболее предпочтительные. Для наблюдения за состоянием магистрали (оценки свойств системы, связанной с закономерностью изменения переменных состояния биообъекта, напряжением организма) целесообразно использовать среднегеометрический показатель [2]:
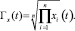
Для равновесного состояния (функционирование в пределах нормы) среднегеометрическое значение равно:
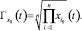
Относительные отклонения среднегеометрического значения биообъекта от равновесных определяется в виде:
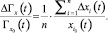
При известных значениях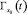 
для интервалов времени, в пределах которых 
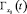остается неизменным, оценкой принадлежности наблюдений к траектории 
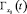является условие:
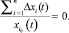
При известных допустимых отклонениях ±∆xmх характер напряженности состояния системы может быть определен на основе относительного изменения среднегеометрических показателей из выражений:
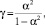
где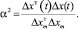 
В данных выражениях 0 ≤ α ≤ 1 и 0 ≤ γ ≤ ∞.
Данная модель позволяет построить траекторию состояния здоровья для некоторой однородной группы детей. Показатели α и γ в этом случае оценивают степень отклонения показателей обследуемого ребенка. При отклонении показателей от 0 можно говорить об напряженности систем организма ребенка.
Заключение
Представленный в статье комплексный подход к прогнозированию состояния здоровья детей, основанный на статистических методах анализа данных, является универсальным и позволяет выявить общие для различных стрессирующих факторов закономерности формирования адаптивного состояния. Прогностический подход способствует наиболее эффективной организации помощи детям, сохранению и укреплению здоровья. Осуществляемый прогноз дает возможность медицинскому персоналу контролировать ход развития ребенка в раннем возрасте и позволяет определить риск и сроки возникновения тех или иных заболеваний.
Исследования проводились по заказу ГУ «Комитет науки Министерства образования и науки Республики Казахстан» в рамках выполнения госбюджетного договора по программе «Грантовое финансирование научных исследований».
Библиографическая ссылка
Гергет О.М., Константинова Л.И., Кочегуров В.А. МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПРОГНОЗИРОВАНИЯ ЗДОРОВЬЯ ДЕТЕЙ РАННЕГО ВОЗРАСТА // Успехи современного естествознания. – 2013. – № 5. – С. 165-169;URL: https://natural-sciences.ru/ru/article/view?id=31740 (дата обращения: 16.04.2024).