Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова

Мазуркин П.М.

Приведены методы ранжирования и рангового моделирования гидрологических параметров у множества крупных рек Земли по примеру статистических данных из учебника.

Статья в формате PDF

190 KB

реки мира

параметры

ранговые распределения

the rivers of the world

the parameters

rank distribution.

По одному «срезу» времени [4, с. 127, табл. 6.1] дается приближенная оценка пределов водных ресурсов крупных рек, причем ресурсы понимаются как научно оправданная доля изъятия пресной воды от среднегодового стока.

Ранжирование параметров. Шаг группировки по рангам зависит от точности измерений гидрологических параметров рек. Шаг ранжирования по данным из первоисточника равен 5 км для длины, 5 км2 для площади и 0,1 км3 для средне
годового стока речной воды. В этом случае одинаковый ранг получают одинаковые значения показателей (табл.1). Авторы учебника [4] строки таблицы расставили по убыванию значений площади водосбора.

Отношение каждого параметра к самому себе дает r_L, r_S и r_Q. Вектор типа «лучше→хуже» у трех гидрологических параметров совпадает: с уменьшением значений параметров L, S и Q происходит ухудшение гидрологических свойств реки из-за изъятия водных ресурсов. Тогда ранги трех параметров суммируются в сумму рангов Σr, по которой расставляются рейтинговые места для каждой крупной реки.

Эту методику можно применить к любым рекам, в том числе и к притокам. При этом количество учитываемых параметров не ограничивается.

Ранговые модели. В монарных отношениях каждый параметр системы крупных рек Земли принимается за независимую переменную. Тогда, в зависимости от своего ранга, получаются следующие закономерности:

длины крупных рек мира (рис. 1)

площади водосборного бассейна крупных рек Земли (рис. 2)

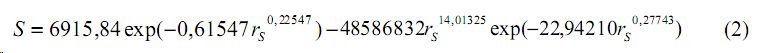
Таблица 1. Параметры крупнейших рек Земли

Примечание: в скобках указаны места по рейтингу

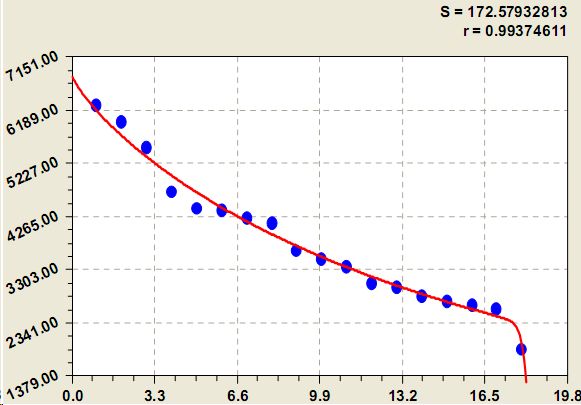
Рис. 1. Ранговое распределение длины крупных рек Земли

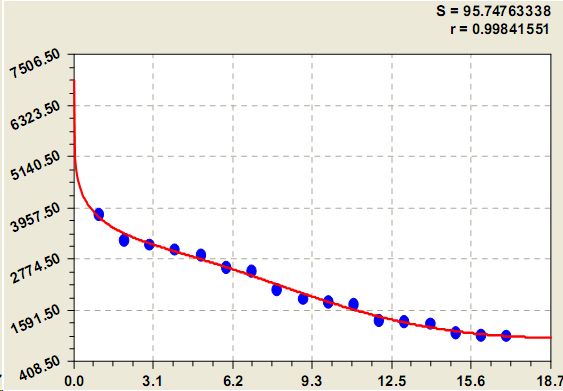
Рис. 2. Ранговое распределение площади водосбора крупных рек

Конструкции уравнений (1) и (2) одинаковы, причем ранговое распределение значений длины становится упрощенным случаем от формулы (2).

Коэффициент корреляцииравен 0,9997 (показан вверху рис. 1), а максимальная относительная погрешность достигает 5,09 %. При этом кризисная вторая составляющая формулы (1) показывает резкое усиление антропогенного влияния с повышением ранга реки, начиная от реки Оранжевая из табл. 1.

По формуле (2) площади бассейнов рек кризисное влияние происходит плавне из-за установления вдоль водотоков водоохранных зон и водозащитных полос.

Модель рангового распределения среднегодового стока речной воды по сравнению с формулой (2) дополняется волновыми составляющими (рис. 3):

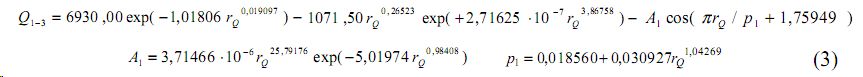
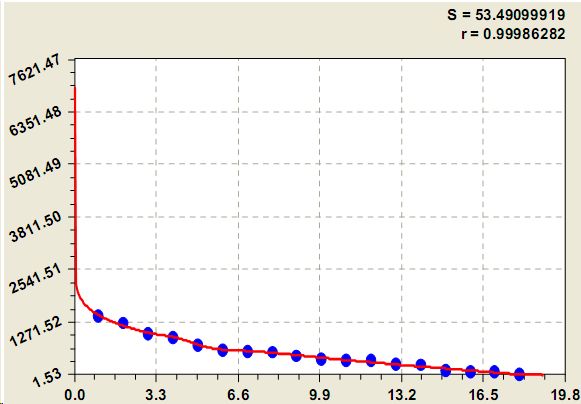
Рис. 3. Ранговое распределение среднегодового стока крупных рек

Первое волновое кризисное возмущение в виде третьей составляющей формулы (3) имеет переменную амплитудночастотную характеристику (АЧХ): A половина амплитуды колебательного возмущения стока у множества крупных рек Земли как некой условной популяции, км³/год; p -половина периода колебательного возмущения среднегодового стока у множества крупных рек в зависимости от природных и антропогенных катастроф.

Параметр Q стока речной воды столь информативен, что оказалось возможным получить еще пять волн возмущения среди 19 крупных рек Земли.

Вторая волна возмущения является вейвлет-сигналом [3] и группирует ранги 9-17 по формуле (рис. 4)

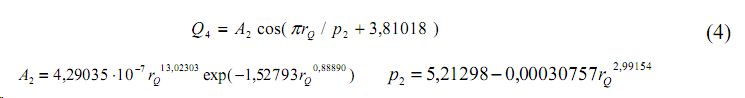
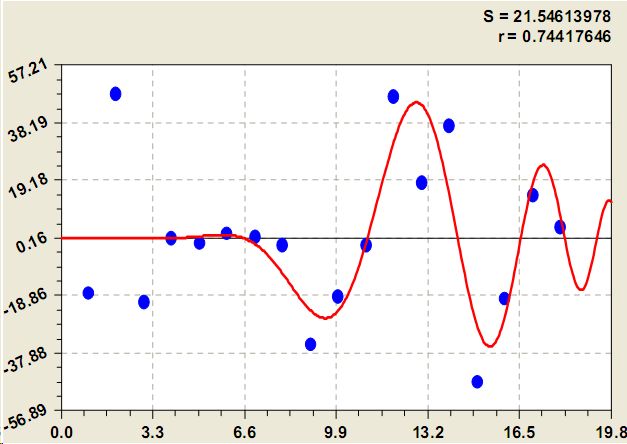
Рис. 4. Ранговое распределение среднегодового стока крупных рек по четвертой составляющей модели

По формуле (4) и рис. 4 река Амур имеет нейтральную позицию среди рангов 9-17, реки Макензи, Нигер, Волга и Нил получили положительную оценку, а реки Св. Лаврентия, Обь, Замбези и Нельсон отрицательную.

В начале ранжированного ряда крупных рек образовалась группка (рис. 5) по формуле сигнала какой-то общности между ними 

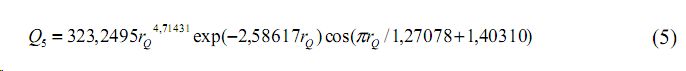
Здесь частота колебания постоянная, но амплитуда возмущения значений у среднегодового стока воды значима для многих средних и малых рек планеты, поэтому формула (5) достоверна и для рек Конго, Ганг и Янцзы.

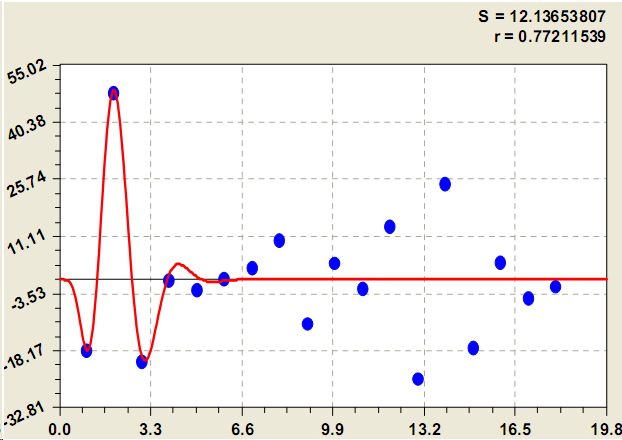
 Рис. 5. Ранговое распределение среднегодового стока крупных рек по пятой составляющей модели

Следующая волна возмущения значений стока относится к рангам 7-17, объединяя их в одну группу (рис. 6) по статистической закономерности вида

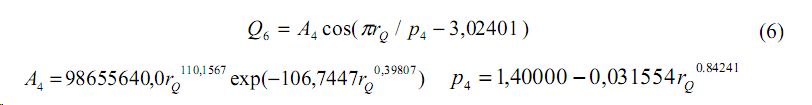
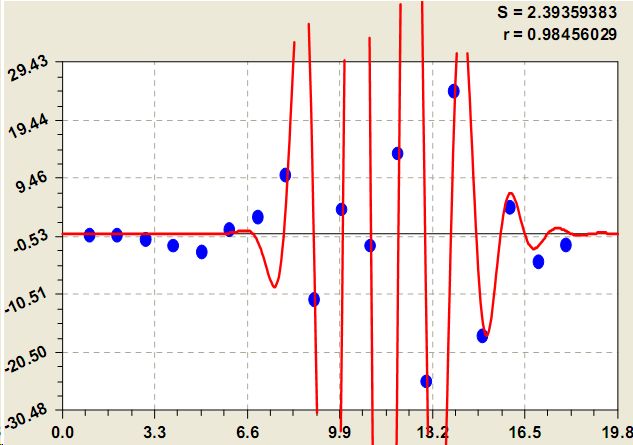
Рис. 6. Ранговое распределение среднегодового стока крупных рек по шестой составляющей модели

Остатки после формулы (6) оказались достаточно высокими, поэтому получилась следующий четкий сигнал (рис. 7) по формуле вейвлет-функции

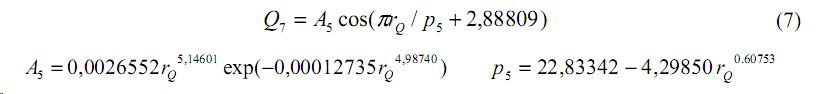
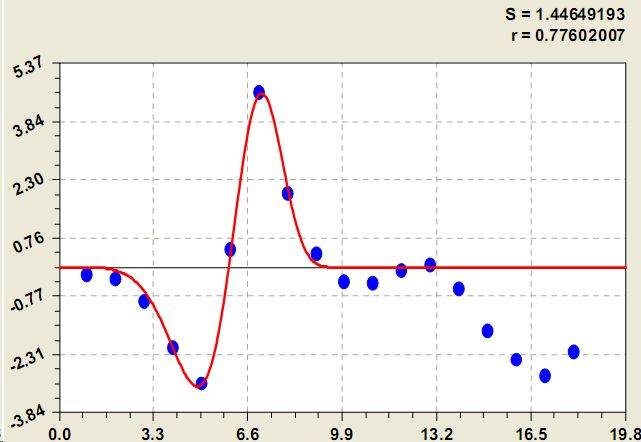
Рис. 7. Ранговое распределение среднегодового стока крупных рек по седьмой составляющей модели

В конце ранжированного ряда крупных рек Земли видно правильное расположение точек. Поэтому восьмая составляющая (рис. 8) получает вид

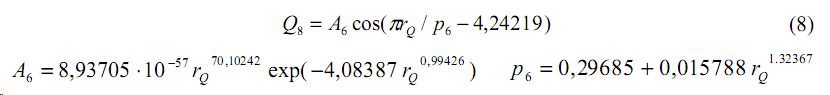
Остатки после модели (8) , показанные на рис. 9, сравнимы со среднегодовыми стоками малых рек. При этом общая статистическая модель получает вид суммы уравнений

Модель (9) имеет высокую адекватность и только водной точке получает максимальную относительную погрешность 0,17 % для реки Оранжевая.

Максимальная  абсолютная  погрешность -0.4394 км3/год наблюдается для реки Амур (ранг 11 по стоку), что в 15,3 / 0,4394 = 34,82 раза меньше по сравнению с рекой Оранжевая.

Из полученной статистической модели (9) рангового распределения среднегодового стока речной воды видно, что для  дальнейшего анализа и установления пределов потребления пресноводных ресурсов необходимо составить список по всем крупным, средним и малым главным рекам Земли, то есть по рекам, впадающим в крупные озера, моря и океаны.

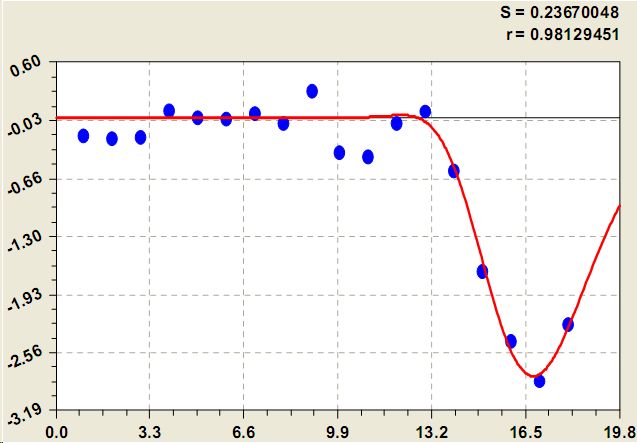
Рис. 8. Ранговое распределение среднегодового стока крупных рек по восьмой составляющей модели

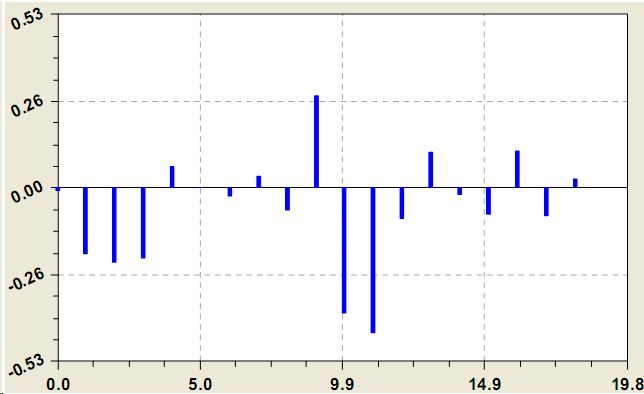
Рис. 9. Остатки после вычислений по модели (9) от факта по табл. 1

СПИСОК ЛИТЕРАТУРЫ:

1. Мазуркин, П.М. Закономерности устойчивого развития: Научное изд. / П.М. Мазуркин. Йошкар-Ола: МарГТУ, 2002. 302с.
2. Мазуркин, П.М. Геоэкология: Закономерности современного естествознания: Научное изд. / П.М. Мазуркин. - Йошкар-Ола: МарГТУ, 2006. - 336 с.
3. Мазуркин, П.М.  Статистическая гидрология:  Учебное  пос.  /  П.М.  Мазуркин, В.И. Зверев, А.И. Толстухин. - Йошкар-Ола: МарГТУ, 2002. - 274 с.
4. Михайлов, В.Н. Общая гидрология: Учебник / В.Н. Михайлов, А.Д. Добровольский. - М.: Высшая школа, 1991. - 368 с.

Статья опубликована при поддержке гранта 3.2.3/4603 МОН РФ

Библиографическая ссылка